Detección de Valores Atípicos Multivariados.
Publicado el: 20 de Enero del 2021 - Jhonatan Montilla
La detección de valores atípicos en datos multivariados a menudo puede ser uno de los desafíos de la fase de preprocesamiento de datos, existen varias métricas, puntuaciones y técnicas para detectar valores atípicos.
La distancia euclidiana, es una de las métricas de distancia más conocidas para identificar valores atípicos en función de su distancia al punto central, también existe el método de la puntuación Z para definir valores atípicos para una única variable numérica, en algunos casos, también se pueden preferir los algoritmos de agrupación en clústeres.
Todos estos métodos consideran valores atípicos desde diferentes perspectivas, los valores atípicos que se encuentran basados en un método pueden no ser encontrados por los demás como valores atípicos, por lo tanto, estos métodos y métricas deben elegirse considerando la distribución de las variables.
Sin embargo, esto resalta las necesidades del uso de diferentes métricas. En este artículo, discutiremos la métrica de la distancia, llamada Distancia de Mahalanobis para detectar valores atípicos en datos multivariados.
Distancia de Mahalanobis.
La distancia de Mahalanobis (MD) es una métrica de distancia efectiva que encuentra la distancia entre un punto y la distribución de los datos, funciona con bastante eficacia en datos multivariados porque utiliza una matriz de covarianza para encontrar la distancia entre los puntos de datos y el centro de la distribución,esto significa que MD detecta valores atípicos basados en el patrón de distribución de puntos de datos, a diferencia de la distancia euclidiana.
La razón principal de esta diferencia es la matriz de covarianza porque la covarianza indica cómo las variables varían juntas, el uso de la covarianza mientras se calcula la distancia entre el centro y los puntos en el espacio n-dimensional permite encontrar el límite del umbral real basado en la variación.
Existe un método para Mahalanobis Distance en la biblioteca "Scipy", se puede acceder a este método desde scipy.spatial.distance.mahalanobis, sin embargo, en lugar de usar este método en los siguientes ejemplos, crearemos nuestro propio método para calcular la Distancia de Mahalanobis.
Se utilizará un conjunto de datos para detectar valores atípicos en las variables "Ozono" y "Temp". Puede descargar el conjunto de datos directamente desde nuestro repositorio haciendo clic aquí.
- Se cargan las librerías y el conjunto de datos.
import pandas as pd
import numpy as np
from scipy.stats import chi2
from matplotlib import patches
import matplotlib.pyplot as plt
df= pd.read_csv('airquality.csv', sep=",", decimal='.' )
df.head()
| Ozone | Solar.R | Wind | Temp | Month | Day | |
|---|---|---|---|---|---|---|
| 0 | 41.0 | 190.0 | 7.4 | 67 | 5 | 1 |
| 1 | 36.0 | 118.0 | 8.0 | 72 | 5 | 2 |
| 2 | 12.0 | 149.0 | 12.6 | 74 | 5 | 3 |
| 3 | 18.0 | 313.0 | 11.5 | 62 | 5 | 4 |
| 4 | NaN | NaN | 14.3 | 56 | 5 | 5 |
df = df[['Ozone', 'Temp']]
df = df.dropna()
df = df.to_numpy()
- Será necesario obtener los valores para calcular la distancia entre el centro y el punto, por lo tanto, estos son el punto central y la matriz de covarianza entre las variables "Ozono" y "Temp".
# Crea la matriz de covarianza
covariance = np.cov(df , rowvar=False)
# Calcula la potencia de la matriz de covarianza de -1
covariance_pm1 = np.linalg.matrix_power(covariance, -1)
# Calcula el punto central
centerpoint = np.mean(df , axis=0)
-
Ahora procederemos a encontrar la distancia entre el punto central y cada observación (punto) en el conjunto de datos. También será necesario encontrar un valor de corte de la distribución Chi-Cuadrado, la razón por la que se utiliza Chi-Cuadrado es para obtener el valor de corte, debido a que la Distancia de Mahalanobis devuelve la distancia al cuadrado (D²).
-
También de debe tomar el valor del cuantil como 0,95 mientras se encuentra el punto de corte debido a que los puntos fuera de 0,95 (de dos colas) se considerarán un valor atípico, menos cuantil significa menos valor de corte, también será necesario obtener un valor de grado de libertad para Chi-Cuadrado, este es igual al número de variables del conjunto de datos, (2).
# Calcula las distancias entre el punto central Y
distances = []
for i, val in enumerate(df):
p1 = val
p2 = centerpoint
distance = (p1-p2).T.dot(covariance_pm1).dot(p1-p2)
distances.append(distance)
distances = np.array(distances)
# Calcula el valor de corte (umbral) de la distribución de chi-cuadrado para detectar valores atípicos
cutoff = chi2.ppf(0.95, df.shape[1])
# Índice de valores atípicos
outlierIndexes = np.where(distances > cutoff )
print("--- Índice de valores atípicos ----\n")
print(outlierIndexes)
print('\n--- Observaciones encontradas como atípicas -----\n')
print(df[ distances > cutoff , :])
--- Índice de valores atípicos ---- (array([24, 35, 67, 81], dtype=int64),) --- Observaciones encontradas como atípicas ----- [[115. 79.] [135. 84.] [122. 89.] [168. 81.]]
# Calcula las dimensiones de la elipse
pearson = covariance[0, 1] / np.sqrt(covariance[0, 0] * covariance[1, 1])
ell_radius_x = np.sqrt(1 + pearson)
ell_radius_y = np.sqrt(1 - pearson)
lambda_, v = np.linalg.eig(covariance)
lambda_ = np.sqrt(lambda_)
# Calcula el relleno de la elipse
ellipse = patches.Ellipse(xy = (centerpoint[0],
centerpoint[1]),
width = lambda_[0] * np.sqrt(cutoff) * 2,
height = lambda_[1] * np.sqrt(cutoff) * 2,
angle = np.rad2deg(np.arccos(v[0, 0])),
edgecolor = '#fab1a0')
ellipse.set_facecolor('#0984e3')
ellipse.set_alpha(0.5)
fig = plt.figure()
ax = plt.subplot()
ax.add_artist(ellipse)
plt.scatter(df[: , 0], df[ : , 1])
plt.show()
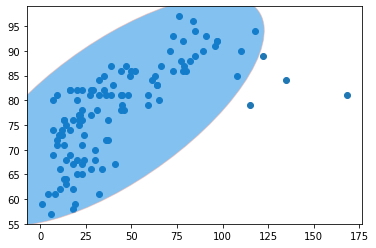
-
Se pueden observar varios puntos fuera de la elipse, esto significa que dichos valores son un valores atípicos, la elipse representa el área que envuelve los valores no atípicos según la Distancia de Mahalanobis.
-
En este artículo hemos aplicado la ecuación de distancia de Mahalanobis en Python desde cero, es importante elegir una métrica de distancia basada en cómo se dispersaron los datos en un espacio de n dimensiones, existe otra métrica de distancia llamada Distancia de Cocción, que profundizaremos en un posterior artículo, esperamos que este les haya sido de ayuda.