Volver al Inicio

• Anterior
• Siguiente

Rotación de Empleados (Churn con Python)

Publicado el: 31 de Enero del 2022 - Jhonatan Montilla

En este caso práctico se analizará la rotación de empleados de una Empresa, se establecerá una hipótesis del por qué los empleados abandonan la Empresa a través de los datos actuales y se realizarán predicciones de cuantos empleados posiblemente abandonarán su cargo.

1. Introducción.

La pérdida de empleados se puede definir como una fuga o salida de un activo intelectual en una Empresa u organización, en palabras simples, cuando un empleado deja la organización se conoce como abandono, posteriormente se deberá reemplazar a este por otro lo que se conoce como rotación.

En varias investigaciones, se descubrió que la rotación de los empleados se verá afectada por la edad, la antigüedad, el sueldo, la satisfacción, las condiciones laborales, el potencial de crecimiento y las percepciones de equidad, otras variables, como la edad, el género, la etnia, la educación y el estado civil, fueron factores importantes en la estimación de la rotación de empleados.

Anteriormente, la mayoría de los departamentos de RRHH se centraba en las "tasas", como la tasa de deserción y las tasas de retención. Los gerentes de RRHH calculaban las tasas anteriores intentado predecir las tasas futuras de abandono, a través de herramientas de almacenamiento de datos. Estas tasas representan un impacto agregado de la deserción, sin embargo, esto no es del todo cierto, debido a que existen otros enfoques que pueden ser el enfoque de registros individuales, así como también, los de agregados.

Existen muchos casos de estudio disponibles sobre la pérdida de clientes, es decir, en la rotación de clientes, en donde predicen cuántos clientes y cuándo dejarán de comprar bienes o servicios. La rotación de empleados es similar a la de clientes, centrándose principalmente en el empleado, con este caso de práctico, podremos predecir quién y cuándo un empleado dejará de prestarle servicios a la Empresa, debido a que la rotación de empleados es costosa para las Empresas y las mejoras incrementales representan un gasto mucho menor, estás mejoras permitirán diseñar mejores planes de incentivos para mejorar en cierta medida la satisfacción del empleado.

En este caso práctico se abordarán los siguientes temas:

• Análisis de rotación de empleados,
• Función de carga y comprensión de datos,
• Análisis exploratorio de datos y visualización de datos,
• Análisis de conglomerados,
• Creación de un modelo de predicción mediante árbol de clasificación y,
• Evaluación del rendimiento del modelo

1.1 Consideraciones Iniciales

Los siguientes puntos ayudarán a comprender mejor la diferencia entre la rotación de empleados y de clientes:

1. La empresa elige al empleado para que contrate a alguien, mientras que en marketing no puede elegir directamente a los clientes.
2. Los empleados serán el rostro de la Empresa y, colectivamente, los empleados producen todo lo que hace la Empresa.
3. La pérdida de un cliente afecta los ingresos y la imagen de marca. Adquirir nuevos clientes es difícil y costoso, en comparación con retener a un cliente existente, la rotación de empleados también es dolorosa para las Empresas. Requiere tiempo y esfuerzo encontrar y capacitar a un reemplazo.
4. La rotación de empleados tiene una dinámica única, en comparación con la rotación de clientes, nos ayuda a diseñar mejores planes de retención de empleados y a mejorar en cierta medida la satisfacción de los mismos.

Los algoritmos de ciencia de datos pueden ayudar a predecir la rotación futura de cierto grupo de empleados que permitan establecer planes para de alguna manera reducirlo o evitarlo.

2. Análisis Exploratorio de Datos.

Se resumirán las características de los datos como patrones, tendencias, valores atípicos y pruebas de hipótesis utilizando estadísticas descriptiva y visualización.

Primeramente, se importan las librerías necesarias a continuación.

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import warnings
warnings.filterwarnings("ignore")

from sklearn.cluster import KMeans
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
from sklearn import metrics
from sklearn.metrics import confusion_matrix

2.1 Carga del Conjunto de Datos.

Se cargan los datos desde un archivo tipo .csv a través de la librería de Pandas. Podrá descargar el conjunto de datos desde nuestro repositorio haciendo clic aquí.

data = pd.read_csv("hhrr_employee_list.csv", encoding = 'latin-1')

• Se revisan los datos iniciales a través de la función head()
• De manera similar, se revisan los datos finales del conjunto de datos a través de la función tail()

data.head()

	Nivel_de_Satisfacción	Última_Evaluación	Cantidad_de_Proyectos	Horas_Promedio_Mensual	Tiempo_en_la_Empresa	Accidentes_Laborales	Abandono	Promoción_Últimos_5_Años	Departamento	Nivel_de_Sueldo
0	0.38	0.53	2	157	3	0	1	0	Ventas	Bajo
1	0.80	0.86	5	262	6	0	1	0	Ventas	Medio
2	0.11	0.88	7	272	4	0	1	0	Ventas	Medio
3	0.72	0.87	5	223	5	0	1	0	Ventas	Bajo
4	0.37	0.52	2	159	3	0	1	0	Ventas	Bajo

data.tail()

	Nivel_de_Satisfacción	Última_Evaluación	Cantidad_de_Proyectos	Horas_Promedio_Mensual	Tiempo_en_la_Empresa	Accidentes_Laborales	Abandono	Promoción_Últimos_5_Años	Departamento	Nivel_de_Sueldo
14994	0.40	0.57	2	151	3	0	1	0	Soporte Técnico	Bajo
14995	0.37	0.48	2	160	3	0	1	0	Soporte Técnico	Bajo
14996	0.37	0.53	2	143	3	0	1	0	Soporte Técnico	Bajo
14997	0.11	0.96	6	280	4	0	1	0	Soporte Técnico	Bajo
14998	0.37	0.52	2	158	3	0	1	0	Soporte Técnico	Bajo

• Se procede a la revisión de las características del conjunto de datos a través de la función info()

data.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 14999 entries, 0 to 14998
Data columns (total 10 columns):
 #   Column                    Non-Null Count  Dtype  
---  ------                    --------------  -----  
 0   Nivel_de_Satisfacción     14999 non-null  float64
 1   Última_Evaluación         14999 non-null  float64
 2   Cantidad_de_Proyectos     14999 non-null  int64  
 3   Horas_Promedio_Mensual    14999 non-null  int64  
 4   Tiempo_en_la_Empresa      14999 non-null  int64  
 5   Accidentes_Laborales      14999 non-null  int64  
 6   Abandono                  14999 non-null  int64  
 7   Promoción_Últimos_5_Años  14999 non-null  int64  
 8   Departamento              14999 non-null  object 
 9   Nivel_de_Sueldo           14999 non-null  object 
dtypes: float64(2), int64(6), object(2)
memory usage: 1.1+ MB

A través de la función info() se obtiene la siguiente información:

• El conjunto de datos contiene 14.999 registros y 10 columnas o características (6 de tipo enteros, 2 de tipo flotantes y 2 de tipo objetos).
• Ninguna columna o característica contiene valores nulos o perdidos.

2.2 Descripción de Características.

• Nivel_de_Satisfacción: Es el porcentaje de satisfacción del empleado en la Empresa (0 a 1),
• Última_Evaluación: Es el porcentaje de desempeño evaluado por el empleador (0 a 1),
• Cantidad_de_Proyectos: Es la cantidad de proyectos asignados al empleado,
• Horas_Promedio_Mensual: Es la cantidad de horas promedio mensual que trabaja un empleado,
• Tiempo_en_la_Empresa: Corresponde al número de años que ha permanecido un empleado en la empresa,
• Accidentes_Laborales: Indica si un empleado ha tenido un accidente laboral o no,
• Abandono: Indica si el empleado ha dejado la Empresa o no, (0: No, 1: Sí),
• Promoción_Últimos_5_Años: Indica si un empleado ha tenido un ascenso en los últimos 5 años o no, (0: No, 1: Sí),
• Departamento: Indica en cual departamento el empleado trabaja y,
• Nivel_de_Sueldo: Indica el nivel de sueldo del empleado, bajo, medio y alto.

2.3 Estadísticas de los Datos

En el conjunto de datos se tienen dos tipos de empleados, uno que permanece y otro que dejó la Empresa, entonces, se pueden dividir los datos en dos grupos para comparar sus características, primeramente analizaremos el promedio de ambos grupos usando las funciones groupby() y mean().

abandono = data.groupby("Abandono")
abandono.mean()

	Nivel_de_Satisfacción	Última_Evaluación	Cantidad_de_Proyectos	Horas_Promedio_Mensual	Tiempo_en_la_Empresa	Accidentes_Laborales	Promoción_Últimos_5_Años
Abandono
0	0.666810	0.715473	3.786664	199.060203	3.380032	0.175009	0.026251
1	0.440098	0.718113	3.855503	207.419210	3.876505	0.047326	0.005321

Con los resultados obtenidos, inicialmente se puede interpretar lo siguiente, los empleados que dejaron la empresa tenían:

• Bajos niveles de satisfacción,
• Baja tasa de promoción y,
• Trabajaron más horas en comparación con los que permanecen en la empresa.

A través de la función describe() de pandas se obtienen varias estadísticas de resumen, la función devuelve:

• Un recuento,
• La media,
• La desviación estándar,
• Los valores mínimo y máximo y,
• Los cuartiles de los datos.

data.describe()

	Nivel_de_Satisfacción	Última_Evaluación	Cantidad_de_Proyectos	Horas_Promedio_Mensual	Tiempo_en_la_Empresa	Accidentes_Laborales	Abandono	Promoción_Últimos_5_Años
count	14999.000000	14999.000000	14999.000000	14999.000000	14999.000000	14999.000000	14999.000000	14999.000000
mean	0.612834	0.716102	3.803054	201.050337	3.498233	0.144610	0.238083	0.021268
std	0.248631	0.171169	1.232592	49.943099	1.460136	0.351719	0.425924	0.144281
min	0.090000	0.360000	2.000000	96.000000	2.000000	0.000000	0.000000	0.000000
25%	0.440000	0.560000	3.000000	156.000000	3.000000	0.000000	0.000000	0.000000
50%	0.640000	0.720000	4.000000	200.000000	3.000000	0.000000	0.000000	0.000000
75%	0.820000	0.870000	5.000000	245.000000	4.000000	0.000000	0.000000	0.000000
max	1.000000	1.000000	7.000000	310.000000	10.000000	1.000000	1.000000	1.000000

De la tabla anterior se puede observar lo siguiente:

• El nivel de satisfacción promedio general (empleados que permanecen y los que abandonaron) es del 61%.
• La evaluación promedio general de los empleados es del casi 72%.
• En la empresa cada empleado maneja en un promedio general 4 proyectos a la vez.
• En la empresa se trabaja en promedio general un poco más de 201 horas al mes, es decir, 41 horas más en promedio de lo establecido.
• En promedio general los empleados permanecen en la empresa casi 3 años y medio.
• El porcentaje de abandono general promedio es de casi 24%.
• La tasa promedio de accidentes general es del 14%, bastante baja.
• El porcentaje de promoción general de empleados es de un poco más del 21%, es considerada baja.

3. Visualización de los Datos.

3.1. Correlación de Variables.

Primeramente, se observará gráficamente cómo se correlacionan las variables entre sí a través de una matriz de correlación de variables numéricas, se determinará el porcentaje positivo o negativo de afectación entre éstas.

# Define la paleta de colores a utilizar
colors_blue = ["#06344d", "#1E90FF", '#00b2ff', '#51C4D3', '#B4DBE9']
sns.palplot(colors_blue)

plt.figure(figsize=(15,10))
sns.heatmap(data.corr(), annot=True, cmap = colors_blue)
plt.title('Correlación de Variables Numéricas\n', weight='bold');

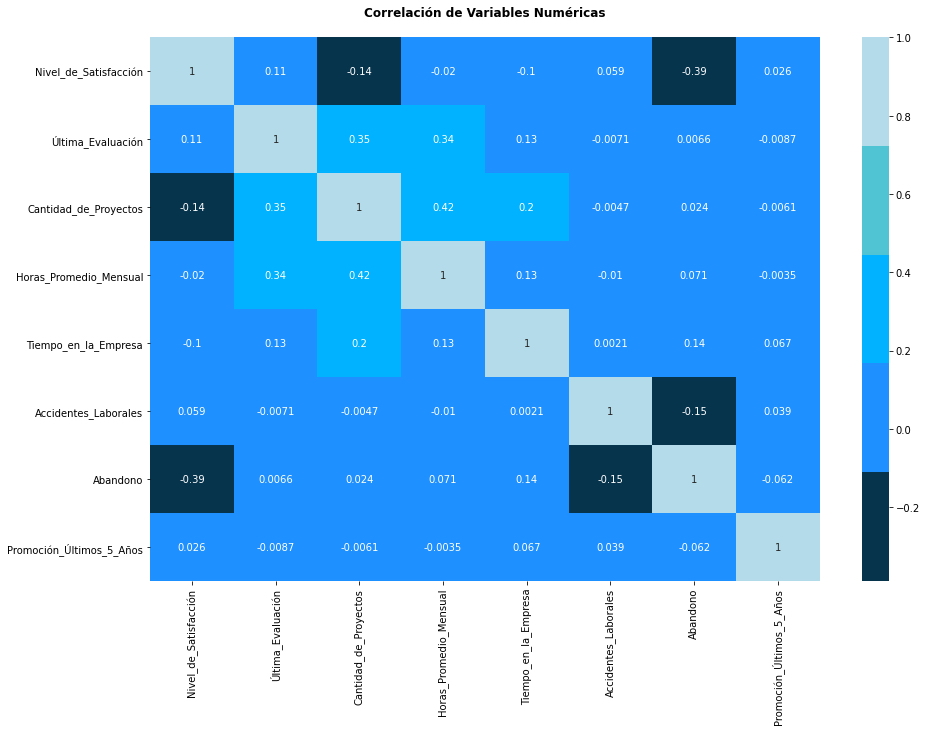
Análisis.

De la matriz de correlación anterior se pueden obtener las siguientes conclusiones.

Afectaciones negativas:

• La Cantidad de Proyectos disminuye el Nivel de Satisfacción en -14%,
• El Nivel de Satisfacción disminuye la cantidad de Abandono en -39%,
• La Cantidad de Accidentes disminuye la cantidad de Abandono en -15% y,
• Las Promociones en los Últimos 5 Años disminuye la cantidad de abandono en -6%.

Afectaciones positivas:

La Cantidad de Proyectos incrementa positivamente,

• La Cantidad de Horas trabajadas en 42%,
• La Última Evaluación del empleado en 35% y,
• La cantidad de Abandono en 24%,

El Tiempo en la Empresa incrementa positivamente,

• La Cantidad de Proyectos en un 20%,
• La cantidad de Abandono en 14%,
• La Última Evaluación en 13% y,
• Las Horas Promedio Mensual trabajadas en 13%, por lo tanto, las Horas Promedio Mensual trabajadas incrementa positivamente la Última Evaluación del empleado en 34%.

3.2 Proporción de permanencia y abandono.

Se representará el porcentaje o cantidad de registros de empleados que permanecen y los que dejaron la Empresa en el actual conjunto de datos, a través del siguiente gráfico:

elem = data.Abandono.value_counts().unique()
elem = elem.tolist() / data.Abandono.count()
elem = elem.tolist()

labels = 'Permanece', 'Abandonó'
sizes = elem

plt.figure(figsize = (7,5))
plt.pie(sizes,
        autopct = '%1.1f%%',
        shadow = True,
        startangle = 90)
plt.title("% de empleados que permanecen \ny que abandonaron la Empresa",
          size = 15,
          y = 1.05)
plt.axis('equal')
plt.legend(labels)
plt.show()

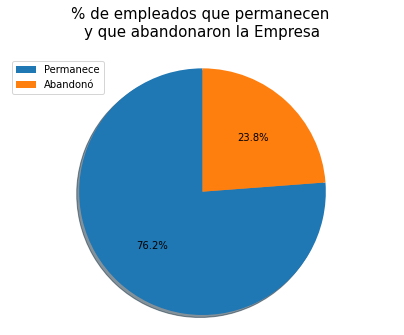
Análisis.

Se puede observar que la cantidad de empleados que permanecen en la Empresa es del 76.2% bastante superior al 23.8% de empleados que abandonaron sus puestos de trabajo, aunque la proporción sea inferior con respecto a la cantidad de empleados que aún trabajan en la Empresa, es importante conocer los niveles de satisfacción y otras variables para cada uno de los grupos, los cuales se revisarán a continuación.

3.3 Nivel de satisfacción general.

Se observará gráficamente la distribución de empleados que permanecen y/o abandonaron la Empresa según el porcentaje del nivel de satisfacción, a través de un histograma de distribución de frecuencias para mostrar el recuento de dichas variables discretas.

plt.figure(figsize = (10,8))
sns.histplot(data = data, x = "Nivel_de_Satisfacción",
             kde = True,
             hue = "Abandono")
plt.title("Distribución de empleados que \npermanecen y abandonaron la Empresa \nsegún el porcentaje satisfacción",
          size = 15, y = 1.04)
plt.xlabel("% de Satisfacción", size = 15)
plt.ylabel("Frecuencia / Empleados", size = 15)
plt.show();

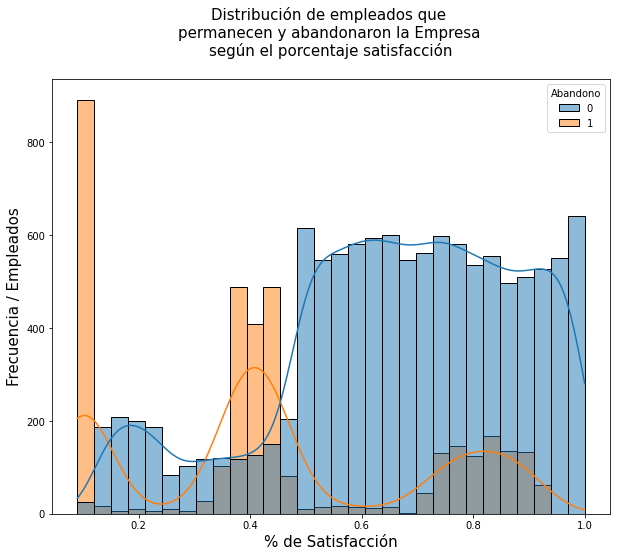
Análisis.

Se puede observar en el gráfico anterior que según la distribución de frecuencias de la satisfacción de empleados que permanecen o dejaron la Empresa es lo siguiente:

• Aproximadamente 900 empleados que abandonaron la Empresa tenían un nivel de satisfacción del 10%,
• Aproximadamente 450 empleados que abandonaron la Empresa tenían un nivel de satisfacción entre el 35% y 45%
• Aproximadamente 200 empleados que abandonaron la Empresa tenían un nivel de satisfacción entre el 80% y 90%

Mientras que:

• Aproximadamente 200 empleados que permanecen en la Empresa tienen un nivel de satisfacción entre el 15% y 25%
• Aproximadamente entre 500 a 600 empleados que permanecen en la Empresa tienen un nivel de satisfacción entre el 50% y 100%.

3.4 Niveles de satisfacción según proyectos asignados.

Se analizará visualmente el porcentaje promedio de satisfacción según la cantidad de proyectos asignados en general, es decir, incluyendo todos los empleados que permanecen y los que abandonaron su cargo en la Empresa.

cant_proyectos = round(data.groupby("Cantidad_de_Proyectos").mean(),2)
plt.figure(figsize = (10,8))
plt.barh(cant_proyectos.index.values,
         cant_proyectos["Nivel_de_Satisfacción"])
for i, v in enumerate(cant_proyectos["Nivel_de_Satisfacción"]):
    plt.text(v + 0.01, i + 1.9, str(v))
plt.xlabel("% de Satisfacción", size = 15)
plt.ylabel("Proyectos", size = 15)
plt.title("% promedio de satisfacción de empleados \nsegún la cantidad de proyectos\nasignados",
          y = 1.05,
          size = 15)
plt.show();

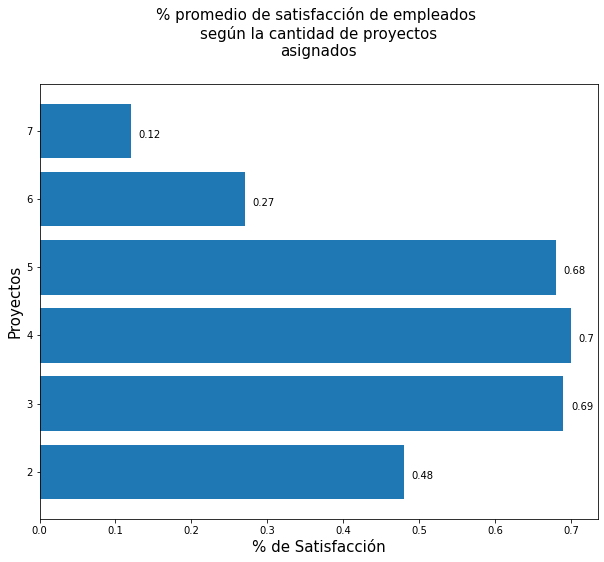
Análisis.

• Los empleados con el menor porcentaje de satisfacción promedio son los que tienen asignados o gestionan 7 proyectos al mismo tiempo, siendo éste el porcentaje promedio más bajo (12%),
• Sin embargo, los empleados que gestionan y administran 4 proyectos al mismo tiempo, registran el mayor porcentaje promedio de satisfacción (70%), se podría inferir que, aunque esos empleados tengan una mayor cantidad de proyectos, no generan un elevado nivel de estrés en ellos,
• Por el contrario, los empleados que administran y gestionan únicamente 2 proyectos a la vez, registran un porcentaje de satisfacción del 48%,
• Se podría decir que los mejores porcentajes promedio de satisfacción se encuentra entre los empleados que gestionan entre 3 y 4 proyectos a la vez.

Con este análisis no se pretende obtener conclusiones finales debido a que no se están evaluando el resto de variables que pueden incidir en la satisfacción del empleado, su permanencia o abandono, por lo que se continuará con el estudio visual del resto de variables.

3.5 Niveles de satisfacción según la cantidad de tiempo en la Empresa (Experiencia).

experiencia = round(data.groupby("Tiempo_en_la_Empresa").mean(),2)
plt.figure(figsize = (10,8))
plt.barh(experiencia.index.values,
         experiencia["Nivel_de_Satisfacción"])
for i, v in enumerate(experiencia["Nivel_de_Satisfacción"]):
    plt.text(v + 0.01, i + 1.9, str(v))
plt.title("% promedio de satisfacción de empleados \nsegún la cantidad de años trabajando\nen la Empresa",
          y = 1.05,
          size = 15)
plt.xlabel("% de satisfacción", size = 15)
plt.ylabel("Años", size = 15)
plt.show();

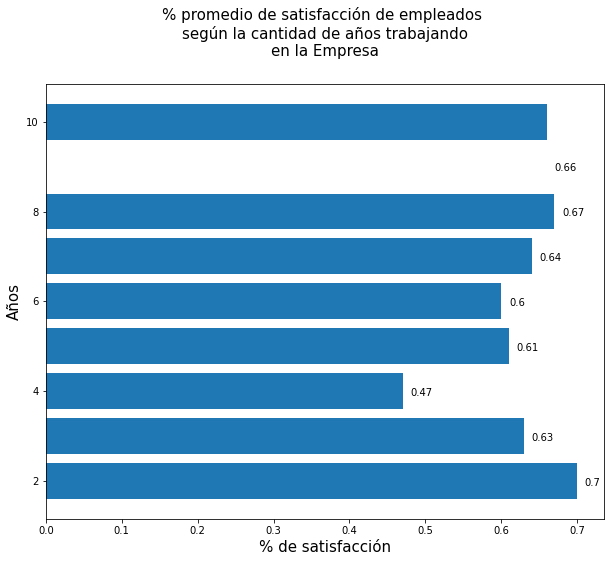
Análisis.

• Se puede observar que el mayor porcentaje promedio de satisfacción se encuentran en los empleados que tienen hasta 2 años trabajando para la Empresa (70%), posteriormente desciende entre los 3 y 4 años.
• Los empleados con 8 y 10 años de experiencia en la empresa tienen un porcentaje promedio de satisfacción bastante similar a la de los empleados con dos años de experiencia, 67% y 66% respectivamente.

La mayor parte de los empleados tienen una experiencia de entre 2 y 4 años. Además, existe una enorme brecha entre 3 y 4 años de empleados con experiencia.

3.6 Totalización de empleados.

Se procederá de manera gráfica, a la totalización y análisis de la cantidad de empleados a través de las siguientes características:

• Por la cantidad de gestión de proyectos a la vez,
• Por el tiempo de experiencia en la Empresa,
• La cantidad de accidentes laborales,
• El abandono (renuncia o dimisión),
• Si ha obtenido al menos una promoción en los últimos 5 años,
• Por departamento al que pertenece y,
• Por el nivel de sueldos.

features = ["Cantidad_de_Proyectos",
            "Tiempo_en_la_Empresa",
            "Accidentes_Laborales",
            "Abandono",
            "Promoción_Últimos_5_Años",
            "Departamento",
            "Nivel_de_Sueldo"]
fig = plt.subplots(figsize=(20,30))
for i, j in enumerate(features):
    plt.subplot(5, 2, i + 1)
    plt.subplots_adjust(hspace = 0.5)
    splot = sns.countplot(x = j, data = data, palette='PuBu')
    for p in splot.patches:
        splot.annotate(format(p.get_height(), '.1f'),
                       (p.get_x() + p.get_width() / 2., p.get_height()),
                       ha = 'center',
                       va = 'bottom',
                       rotation = 90,
                       xytext = (0, 9),
                       textcoords = 'offset points')
    plt.xticks(rotation = 90)
    plt.ylabel("Cantidad de empleados")
    plt.xlabel("")
    plt.title(j, y = 1.2);

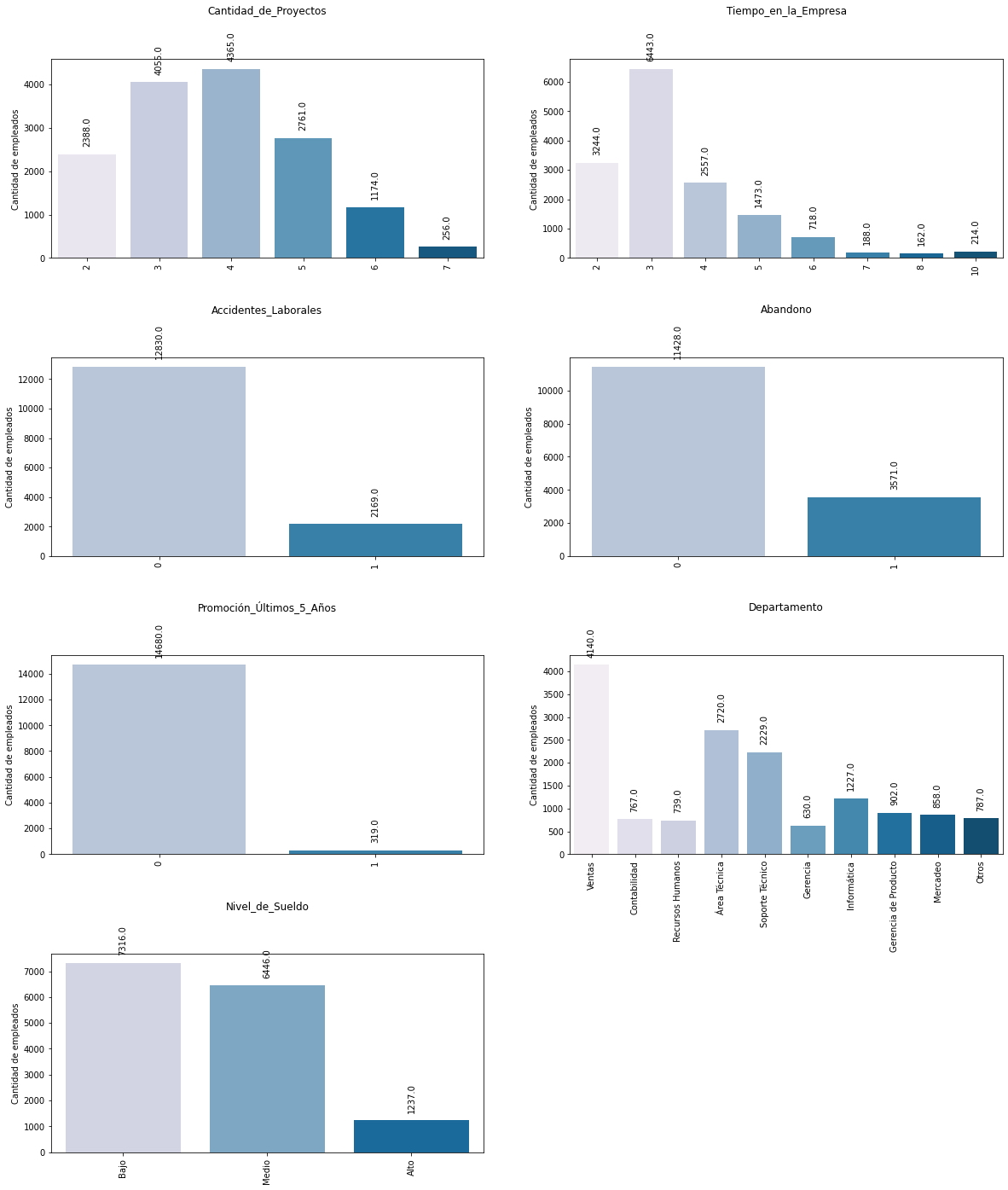
Análisis.

De los gráficos anteriores se puede concluir lo siguiente:

• La mayor cantidad de empleados se encuentran trabajando en 4 proyectos al mismo tiempo (4.365 empleados),
• La mayor cantidad de empleados tienen tres años trabajando para la Empresa (6.443 empleados),
• Únicamente 2.169 empleados han tenido algún accidente laboral.
• Únicamente 3.571 empleados han abandonado sus puestos de trabajo en la Empresa,
• Únicamente 319 empleados han obtenido al menos una promoción en los últimos 5 años,
• La mayor cantidad de empleados se encuentran trabajando en el departamento de ventas (4.140 empleados), seguido por los de área técnica con 2.720 empleados,
• En el nivel más bajo de sueldos se encuentra la mayoría de los empleados (7.316 empleados), mientras que únicamente 1.237 empleados obtienen los sueldos más altos.

3.7 Proporción de empleados.

En esta sección se procederá al análisis de las proporciones de empleados según alguno de los grupos señalados en los gráficos anteriores.

def element (df, col):
    elem = df[col].value_counts().unique()
    elem = elem.tolist() / df[col].count()
    elem = elem.tolist()
    return elem

def donas (df,labs,titl):
    plt.pie(df,
             autopct = '%1.1f%%',
             startangle = 90,
             pctdistance = 0.85)
    plt.title(titl, size = 16, y = 1.05)
    plt.legend(labs)
    centre_circle = plt.Circle((0,0),0.60, fc = 'white')
    fig = plt.gcf()
    fig.gca().add_artist(centre_circle)
    plt.axis('equal')  
    plt.tight_layout()
    plt.show();

elem = element(data,"Cantidad_de_Proyectos")
donas(elem,
      ["1 Proyecto", "2 Proyectos","3 Proyectos","4 Proyectos","5 Proyectos","6 Proyectos","7 Proyectos"],
      "% de empleados que trabajan en \nvarios proyectos a la vez")

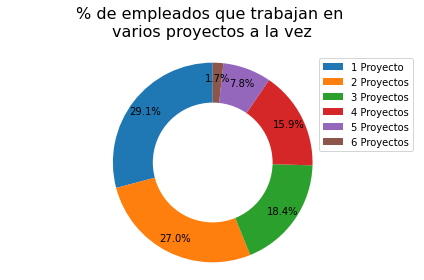
Análisis.

Se puede observar en el gráfico anterior que:

• El 29.1% de los empleados tienen asignado un único proyecto,
• El 27% de los empleados tienen asignados dos proyectos simultáneamente,
• Por lo tanto, el 56.1% del total de empleados tienen asignados menos o igual a dos proyectos simultáneamente,
• Únicamente el 1.7% del total de empleados tienen asignados seis proyectos simultáneamente.

elem = element(data,"Tiempo_en_la_Empresa")
donas(elem,
      ["1 Año", "2 Años","3 Años","4 Años","5 Años","6 Años","7 Años","8 Años","9 Años","10 Años"],
      "% de empleados que tienen tantos \naños de experiencia trabajando \nen la empresa")

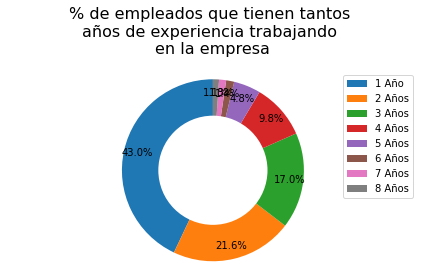
Análisis.

Se puede observar en el gráfico anterior que:

• El 43% del total de empleados tiene tan solo un año de experiencia trabajando en la Empresa,
• El 21.6% del total de empleados tiene un par de años de experiencia trabajando en la Empresa,
• Por lo tanto, el 64.6% del total de empleados tienen menos o igual a dos años de experiencia trabajando en la Empresa.

elem = element(data,"Promoción_Últimos_5_Años")
donas(elem,
      ["No", "Si",],
      "% de empleados que obtivieron al menos una \npromoción en los últimos 5 años")

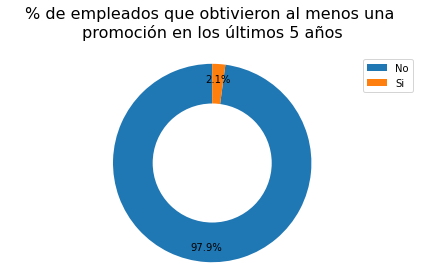
Análisis.

• Es evidente que la mayoría de los empleados no han recibido al menos una promoción en los últimos cinco años, sin embargo, es importante señalar, como se pudo observar en el gráfico anterior, el 91.4% del total de empleados no superan los cuatro años de experiencia trabajando dentro de la Empresa.

• Por lo tanto, será necesario analizar cuantos del 8.6% restante superan los cinco años de experiencia y si obtuvieron o no un ascenso o promoción.

elem = element(data,"Nivel_de_Sueldo")
donas(elem,
      ["Bajo", "Medio","Alto"],
      "% del total de empleados con distintos niveles \nde sueldos")

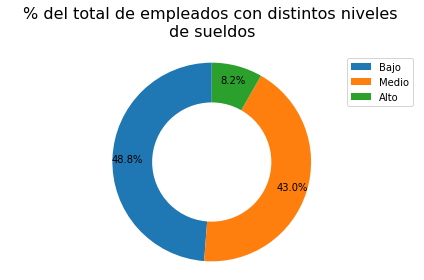
Análisis.

• Se puede observar que el 48% del total de empleados obtiene sueldos bajos y el 43% obtiene sueldos medios.

3.8 Niveles de satisfacción según niveles de sueldos (Variable Categórica).

def show_values_on_bars(axs):
    def _show_on_single_plot(ax):        
        for p in ax.patches:
            _x = p.get_x() + p.get_width() / 2
            _y = p.get_y() + p.get_height() + 5
            value = '{:.2f}%'.format(p.get_height())
            ax.text(_x, _y, value, ha="center") 
    if isinstance(axs, np.ndarray):
        for idx, ax in np.ndenumerate(axs):
            _show_on_single_plot(ax)
    else:
        _show_on_single_plot(axs)

df = data
df_ = df["Nivel_de_Satisfacción"] * 100
df["Nivel_de_Satisfacción"] = df_

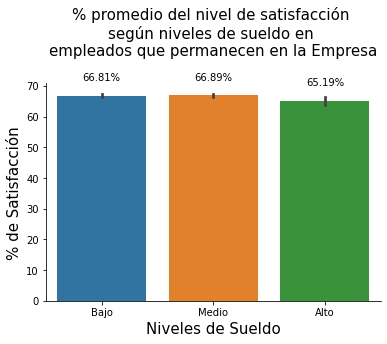
fig, ax = plt.subplots(1, 1)
sns.barplot(x = "Nivel_de_Sueldo",
            y = "Nivel_de_Satisfacción",
            data = df[df["Abandono"]==0],
            )
sns.despine(bottom = False, left = False)
plt.title("% promedio del nivel de satisfacción \nsegún niveles de sueldo en \nempleados que permanecen en la Empresa",
          size = 15,
          y = 1.1)
plt.xlabel("Niveles de Sueldo", size = 15)
plt.ylabel("% de Satisfacción", size = 15)
show_values_on_bars(ax)

fig, ax = plt.subplots(1, 1)
sns.barplot(x = "Nivel_de_Sueldo",
            y = "Nivel_de_Satisfacción",
            data = df[df["Abandono"]==1])
sns.despine(bottom = False, left = False)
plt.title("% promedio del nivel de satisfacción \nsegún niveles de sueldo en \nempleados que abandonaron la Empresa",
          size = 15,
          y = 1.1)
plt.xlabel("Niveles de Sueldo", size = 15)
plt.ylabel("% de Satisfacción", size = 15)
show_values_on_bars(ax)

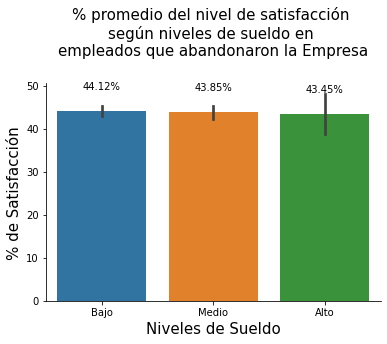
Análisis.

De los dos gráficos anteriores se puede concluir los siguiente.

Empleados que abandonaron la Empresa:

• El porcentaje del nivel de satisfacción se encuentra aproximadamente en un 20% por debajo de los empleados que permanecen, independientemente del nivel de sueldo y,
• El porcentaje de satisfacción más bajo se registra para empleados con los niveles de sueldo más altos con 43.45%, seguido por los de sueldos medios con 43.85% y, finalmente con 44.12% de satisfacción para los empleados con sueldos más bajos, esto podría indicar que los empleados que recibieron sueldos altos no se encontraban satisfechos con sus ingresos, aunque obtenían los sueldos más altos.

Empleados que permanecen en la Empresa:

• El porcentaje de satisfacción mayor se encuentra en el grupo con sueldos medios con 66.89%, seguido por los de sueldos más bajos con 66.81% y, finalmente por los de sueldos más altos con 65.19%. Esto podría indicar que los empleados con los sueldos altos se encuentran menos satisfechos con sus ingresos en comparación con el nivel de satisfacción de empleados con sueldos medios y bajos.

3.9 Promociones (Empleados con 5 años o más de experiencia).

En esta sección se analizará el porcentaje de empleados que tienen cinco o más años de experiencia trabajando en la Empresa.

data_5 = data[data["Tiempo_en_la_Empresa"] >= 5] # Crea un conjunto de datos filtrado
# Confirma que efectivamente el conjunto de datos filtrado
# corresponde a empleados con 5 años o más de experiencia
# trabajando en la Empresa
data_5.Tiempo_en_la_Empresa.unique()

array([ 6,  5,  8, 10,  7], dtype=int64)

elem = element(data_5,"Promoción_Últimos_5_Años")
donas(elem,
      ["No", "Si",],
      "% empleados con 5 años o más que obtivieron \nal menos una promoción ")

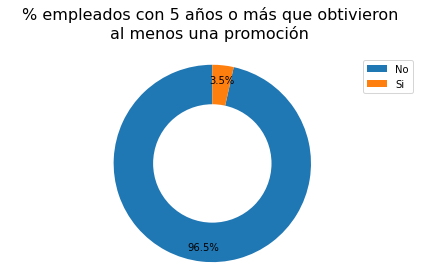
print("Cantidad de empleados con promoción: ",
      data_5[data_5["Promoción_Últimos_5_Años"]==1].Promoción_Últimos_5_Años.count())
print("Cantidad de total empleados con 5 años o más de experiencia: ",
      data[data["Tiempo_en_la_Empresa"] >= 5].Promoción_Últimos_5_Años.count())

Cantidad de empleados con promoción:  96
Cantidad de total empleados con 5 años o más de experiencia:  2755

Análisis.

• Se puede observar que del total de empleados que tienen cinco años o más de experiencia trabajando en la Empresa, únicamente el 3.5% obtuvo al menos un ascenso o promoción, es decir, de un total de 2.755 empleados con cinco años de experiencia o más trabajando en la empresa, únicamente 96 han obtenido al menos una promoción.

3.10 Contraste de Empleados.

Al igual que la sección anterior de Totalización de Empleados se procederá de manera gráfica, a la totalización y análisis de la cantidad de empleados realizando una comparación de cantidades entre los empleados que abandonaron sus puestos de trabajo y los que aún permanecen en la Empresa.

fig = plt.subplots(figsize = (20,30))
for i, j in enumerate(features):
    plt.subplot(5, 2, i + 1)
    plt.subplots_adjust(hspace = 0.5)
    splot = sns.countplot(x = j,data = data, palette='PuBu', hue = "Abandono")
    for p in splot.patches:
        splot.annotate(format(p.get_height(), '.1f'),
                       (p.get_x() + p.get_width() / 2., p.get_height()),
                       ha = 'center',
                       va = 'bottom',
                       rotation = 90,
                       xytext = (0, 9),
                       textcoords = 'offset points')
    plt.xticks(rotation = 90)
    plt.ylabel("Cantidad de empleados")
    plt.xlabel("")
    plt.title(j, y = 1.2);

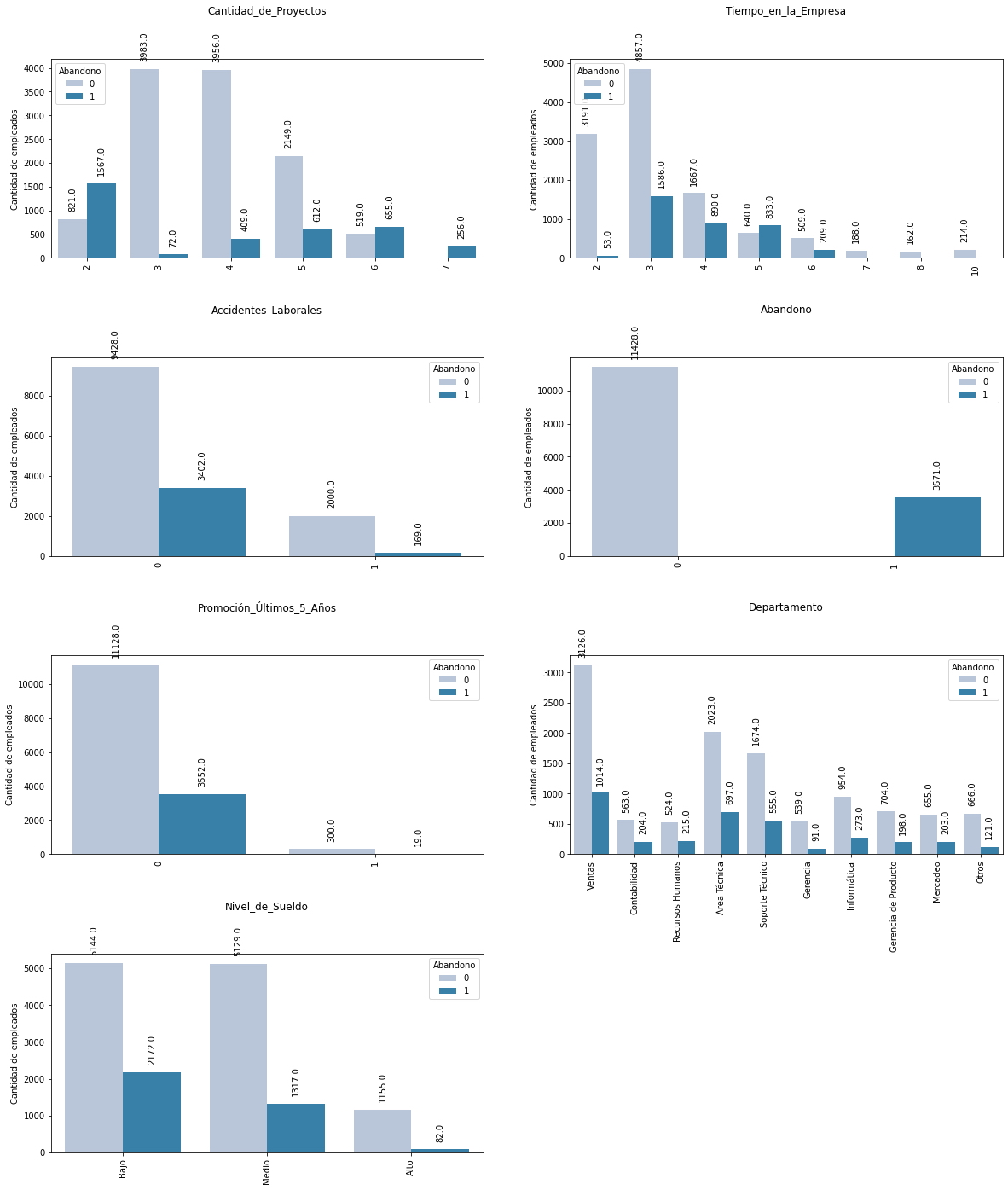
Análisis.

• Según la cantidad de proyectos asignados: Se puede observar que la mayoría de empleados que abandonaron sus cargos fueron empleados (1.567 empleados) con únicamente dos proyectos asignados al mismo tiempo, muy superior al número de empleados (256 empleados) que abandonaron sus puestos de trabajo con siete proyectos asignados al mismo tiempo.

• Según los años de experiencia en la empresa: Se puede observar que la mayoría de los empleados (1.586 empleados) que abandonaron sus puestos de trabajo tenían al menos tres años de experiencia, por lo que es claro que la mayoría de los empleados que abandonaron sus puestos de trabajo no hayan obtenido al menos una promoción o ascenso (3.552 empleados).

• Según el departamento: Se puede observar que la mayoría de los empleados que abandonaron sus puestos de trabajo se encuentran en el departamento de ventas (1.014 empleados), esto se debe a que en ese departamento es donde se encuentra la mayoría de empleados, tal como se observó en la sección de gráficos, Totalización de Empleados.

• Según el nivel de sueldo: Se puede observar que la mayoría de los empleados que abandonaron sus puestos de trabajos se encuentran en el grupo con los sueldos más bajos (2.172 empleados).

Antes de finalizar la sección de análisis exploratorio de datos con gráficos, para obtener un enfoque más amplio, veremos un aspecto fundamental en el análisis de los datos, el análisis de conglomerados (clusterización).

3.11 Análisis de conglomerados:

Será necesario analizar más el grupo de empleados que abandonaron sus puestos de trabajo, como se ha observado en los gráficos anteriores, el factor más importante para que cualquier empleado que permanezca o abandone la Empresa depende del nivel de satisfacción personal y su desempeño en la Empresa, por lo tanto, se procederá a agruparlos para realizar un análisis de conglomerados o de clusterización.

# Se filtran los datos (únicamente empleados que abandonaron)
abandona_emp =  data[['Nivel_de_Satisfacción', 'Última_Evaluación']][data.Abandono == 1]
# Se crean los grupos usando K-means
clustering_kmeans = KMeans(n_clusters = 3,
                           random_state = 0).fit(abandona_emp)
# Se agrega una nueva columna "etiqueta" y se asigna por grupo.
abandona_emp['etiqueta'] = clustering_kmeans.labels_
# Se crea el diagrama de dispersión
plt.figure(figsize = (15,10))
plt.scatter(abandona_emp['Nivel_de_Satisfacción'],
            abandona_emp['Última_Evaluación'],
            c = abandona_emp['etiqueta'],
            cmap = 'Accent'
           )
plt.xlabel("% de satisfacción", size = 15)
plt.ylabel("% de desempeño según \núltima evaluación", size = 15)
plt.title("Clusterización de empleados \nque abandonaron la Empresa", y = 1.05, size = 15)
plt.show();

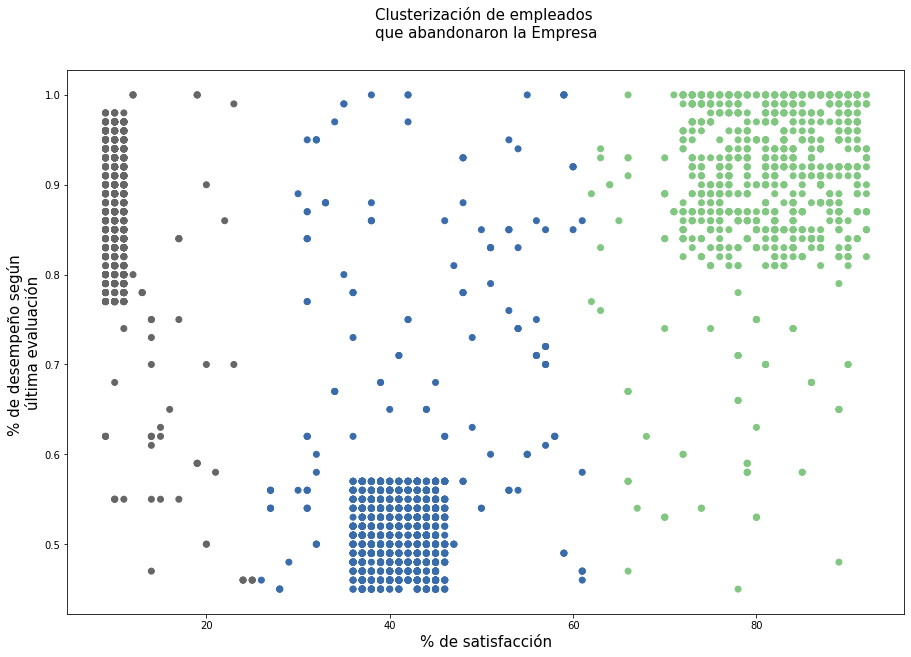
Análisis.

El empleado que abandonó la empresa se puede clasificar en tres tipos de empleados:

• Empleados con alta satisfacción y alta evaluación, puntos en color verde, se pueden clasificar como "Los Ganadores",
• Empleados con baja satisfacción y alta evaluación, puntos en color gris, se pueden clasificar como "Los Frustrados" y,
• Empleados con satisfacción moderada y evaluación moderada, puntos en color azul, se pueden clasificar como "Los No Comprometidos".

4. Construcción del Modelo de Predicción.

4.1 Datos de preprocesamiento

Muchos algoritmos de aprendizaje automático requieren datos de entrada numéricos, por lo que será necesario transformar las columnas categóricas en columnas numéricas. Para la codificación de los datos, se asignará cada categoría a un número, por ejemplo, el valor de la columna de nivel de sueldos se puede representar como: Bajo: 0, Medio: 1 y Alto: 2. Este proceso se conoce como codificación, haciendo uso de la librería SkLearn convenientemente lo hará la función LabelEncoder().

data = pd.read_csv("hhrr_employee_list.csv", encoding = 'latin-1')
# Se crea el codificador
le = preprocessing.LabelEncoder()
# Se transforman las etiquetas en números.
data['Nivel_de_Sueldo'] = le.fit_transform(data['Nivel_de_Sueldo'])
data['Departamento'] = le.fit_transform(data['Departamento'])

print("Departamentos: ",
      data.Departamento.unique(),
      "\nNiveles de sueldo: ", data.Nivel_de_Sueldo.unique())

Departamentos:  [8 0 6 9 7 1 3 2 4 5] 
Niveles de sueldo:  [1 2 0]

El procedimiento anterior importó el módulo de preprocesamiento, se creó el objeto LabelEncoder, con este se ajustaron y se transformaron las columnas "Nivel_de_Sueldo" y "Departamento" en columnas numéricas.

4.2 División del conjunto de datos (Train, Test)

Para comprender el rendimiento del modelo, se procede a dividir el conjunto de datos en un conjunto de entrenamiento y otro conjunto de pruebas, a través del uso de la función train_test_split().

# Se dividen los datos según características
X = data[["Nivel_de_Satisfacción",
          "Última_Evaluación",
          "Cantidad_de_Proyectos",
          "Horas_Promedio_Mensual",
          "Tiempo_en_la_Empresa",
          "Accidentes_Laborales",
          "Promoción_Últimos_5_Años",
          "Departamento",
          "Nivel_de_Sueldo"]]
y = data["Abandono"]
# Se divide el conjunto de datos en un conjuntos
# de entrenamiento y pruebas (70% de entrenamiento
# y 30% de prueba)
X_train, X_test, y_train, y_test = train_test_split(
    X,
    y,
    test_size = 0.3,
    random_state = 42
)

El conjunto de datos se dividió en dos partes en una proporción de 70:30, es decir,70% de los datos se utilizarán para el entrenamiento de modelo y el 30% para las pruebas.

4.3 Construcción del modelo

En esta sección se construirá un modelo para predicción de abandono de empleados, este será capaz de predecir la deserción haciendo uso de la función GradientBoostingClassifier(), primeramente se importará el módulo, posteriormente se creará el objeto clasificador, seguidamente se ajustará el modelo al conjunto de entrenamiento a través de la función fit(), para finalmente realizar predicciones, y a través del conjunto de pruebas evaluarlas.

# Se crear el clasificador de aumento de gradiente
gb = GradientBoostingClassifier()
# Se entrena el modelo con el conjunto de entrenamiento
gb.fit(X_train, y_train)
# Se realizan las predicciones para el conjunto de
# datos de prueba
y_pred = gb.predict(X_test)

4.4 Predicciones del Modelo

4.4.1 Matriz de Confusión

A través de una matriz de confusión se podrá observar visualmente la cantidad de aciertos en la predicción del modelo

matriz = confusion_matrix(y_test, y_pred)
group_counts = ["{0:0.0f}".format(value) for value in
                matriz.flatten()]
group_percentages = ["{0:.2%}".format(value) for value in
                     matriz.flatten()/np.sum(matriz)]
labels = [f"{v1}\n{v2}" for v1, v2 in
          zip(group_counts,group_percentages)]
labels = np.asarray(labels).reshape(2,2)
ax = sns.heatmap(matriz,
                 annot = labels,
                 fmt = '',
                 cmap='Blues')
ax.set_title("Matriz de Confución para \nevaluación del modelo\n\n");
ax.set_xlabel("\nValores Predichos")
ax.set_ylabel("Valores Reales");
ax.xaxis.set_ticklabels(['Permanece','Abandona'])
ax.yaxis.set_ticklabels(['Permanece','Abandona'])
plt.show();

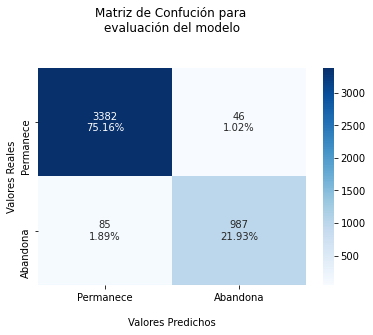
Análisis.

Según el gráfico anterior de la matriz de confusión, se pude concluir los siguiente:

• De un total de 3.428 empleados que aparecen clasificados en el conjunto de datos de pruebas, que permanecen en la Empresa, el modelo predijo que 3.382 empleados permanecerán (acertando 75.16%) y 46 empleados abandonarán (fallando 1.02%).
• De un total de 1.072 empleados que aparecen clasificados en el conjunto de datos de pruebas, que abandonaron la Empresa, el modelo predijo que 987 (acertando 21.93%) empleados abandonarán y 85 (fallando 1.89%) empleados permanecerán.

Para entender que significan estas predicciones del modelo será necesario entender sus niveles de exactitud y precisión, las cuales se analizarán a continuación.

4.4.2 Evaluación y Métricas

En esta sección se evaluará la exactitud, y la precisión del modelo haciendo uso de las funciones de métricas metrics.accuracy_score(), metrics.precision_score() y, evaluación del modelo a través del conjunto de pruebas con la función metrics.recall_score().

print("Exactitud: ",metrics.accuracy_score(y_test, y_pred))
print("Precisión: ",metrics.precision_score(y_test, y_pred))
print("Evaluación: ",metrics.recall_score(y_test, y_pred))

Exactitud:  0.9708888888888889
Precisión:  0.9554695062923524
Evaluación:  0.9207089552238806

5. Conclusiones

• En la exactitud, a través de este modelo se obtiene una tasa de clasificación con exactitud general de 97%, se considera un alto índice de exactitud,
• En la predicción, cuando el modelo predice que algún número de empleados abandonarán la Empresa, éste tendrá una precisión general del 95% de las veces.
• En la evaluación, si hay un empleado clasificado como que permanece en la Empresa en el conjunto de pruebas, el modelo es capaz de identificarlo en general el 92% de las veces.

A través de este caso de uso se ha podido estudiar de manera bastante completa un caso de abandono de empleados, desde el análisis exploratorio de datos, la creación de un modelo de clasificación y predicción, como se comentó al inicio, este modelo también se podría utilizar para la predicción de abandono de clientes, tomando en consideración que habría que realizar un análisis exploratorio de datos para ese caso en particular.

El empleado es como con un nicho, donde sus habilidades son más difíciles de reemplazar, esto afecta el trabajo continuo y la productividad de los empleados existentes, la adquisición de nuevos empleados como reemplazo, tiene sus propios costos, como los costos de contratación, costos de capacitación entre otros, además, el nuevo empleado se tomará un tiempo para adquirir las habilidades a un nivel similar de conocimiento técnico o de experiencia comercial de un empleado con mayor tiempo en la Empresa, por esta razón este caso de uso ayudará a la organización para abordar este problema a través de aplicar las técnicas de aprendizaje automático implementadas, para predecir la rotación de empleados, lo que les permitirá a tomar las medidas necesarias.