Volver al Inicio

• Anterior
• Siguiente

Funcionamiento del Aprendizaje Automático (Machine Learning).

Publicado el: 19 de Diciembre del 2021 - Jhonatan Montilla

Python para la Ciencia de Datos | Imágen Crédito: Meritude Udyog Kendra

Mucha gente dice que los modelos de aprendizaje automático son "cajas negras", en el sentido de que pueden hacer buenas predicciones, pero no se puede entender la lógica detrás de esas predicciones. Esta afirmación es cierta en el sentido de que la mayoría de los científicos de datos aún no saben cómo extraer conocimientos de los modelos. Sin embargo, en este caso de estudio veremos técnicas para extraer los siguientes conocimientos de modelos sofisticados de aprendizaje automático.

• ¿Cuales características de los datos consideró el modelo más importantes?,
• Para cualquier predicción única de un modelo, ¿cómo afectó cada característica de los datos a esa predicción en particular?,
• ¿Cómo afecta cada característica a las predicciones del modelo en un sentido general (cuál es su efecto típico cuando se considera sobre una gran cantidad de predicciones posibles)?.

¿Por qué son valiosos estos conocimientos?.

Estos conocimientos tienen muchos usos, incluyendo:

• La depuración,
• La creación de ingeniería de características,
• La recopilación de datos en el futuro,
• La toma de decisiones humanas y,
• La creación de confianza.

La Depuración.

El mundo tiene una gran cantidad de datos poco fiables, desorganizados y, en general, sucios. Se agrega una fuente potencial de errores a medida que se escribe código de preprocesamiento. También se agregua el potencial de fuga de objetivos, y es la norma, más que la excepción, tener errores en algún momento en un proyecto de ciencia de datos real. Dada la frecuencia y las consecuencias potencialmente desastrosas de los errores, la depuración es una de las habilidades más valiosas en la ciencia de datos. Comprender los patrones que encuentran un modelo le ayudará a identificar cuándo están en desacuerdo con su conocimiento del mundo real, y este suele ser el primer paso para rastrear errores.

La creación de ingeniería de características.

La ingeniería de características suele ser la forma más eficaz de mejorar la precisión del modelo. La ingeniería de características generalmente implica la creación repetida de nuevas características utilizando transformaciones de sus datos sin procesar o características que ha creado previamente. A veces, puede pasar por este proceso utilizando nada más que la intuición sobre el tema subyacente. Pero necesitará más dirección cuando tenga cientos de funciones en bruto o cuando no tenga conocimientos básicos sobre el tema en el que está trabajando. A medida que un número creciente de conjuntos de datos comienza con cientos o miles de características sin procesar, este enfoque se vuelve cada vez más importante.

La recopilación de datos en el futuro.

No tienes control sobre los conjuntos de datos que descargas en línea. Pero muchas empresas y organizaciones que utilizan la ciencia de datos tienen la oportunidad de ampliar los tipos de datos que recopilan. La recopilación de nuevos tipos de datos puede ser costosa o inconveniente, por lo que solo quieren hacer esto si saben que valdrá la pena. Los conocimientos basados en modelos le brindan una buena comprensión del valor de las funciones que tiene actualmente, lo que lo ayudará a razonar sobre qué nuevos valores pueden ser más útiles.

La toma de decisiones humanas.

Algunas decisiones las toman los modelos automáticamente. Amazon no tiene humanos (o elfos) que se apresuren a decidir qué mostrarle cada vez que visite su sitio web. Pero los humanos toman muchas decisiones importantes. Para estas decisiones, los conocimientos pueden ser más valiosos que las predicciones.

La creación de confianza.

Muchas personas no asumirán que pueden confiar en su modelo para tomar decisiones importantes sin verificar algunos hechos básicos. Esta es una precaución inteligente dada la frecuencia de errores de datos. En la práctica, mostrar conocimientos que se ajusten a su comprensión general del problema ayudará a generar confianza, incluso entre personas con poco conocimiento profundo de la ciencia de datos.

Permutación de características.

Una de las preguntas más básicas que podríamos plantearnos a un modelo es: ¿Qué características tienen el mayor impacto en las predicciones?, Este concepto se llama importancia de la característica. Hay varias maneras de medir la importancia de las características. Algunos enfoques responden a versiones sutilmente diferentes de la pregunta anterior. Otros enfoques tienen deficiencias documentadas. En este caso de estudio, nos centraremos en la importancia de la permutación de las características. En comparación con la mayoría de los otros enfoques, la importancia de la permutación es:

• Rápido de calcular,
• Ampliamente utilizado y entendido, y
• Coherente con las propiedades que quisiéramos que tuviera una medida de importancia de característica.

Funcionamiento.

La importancia de la permutación usa modelos de manera diferente a cualquier cosa que haya visto hasta ahora, y muchas personas lo encuentran confuso al principio. Para entenderlo mejor realizaremos el siguiente ejemplo. Queremos predecir la altura de una persona cuando cumpla 20 años, utilizando datos que están disponibles a los 10 años. Nuestros datos incluyen características útiles (altura a los 10 años), características con poco poder predictivo (calcetines propios), así como algunas otras características en las que no nos centraremos en esta explicación. La importancia de la permutación se calcula después de que se ha ajustado un modelo. Por lo tanto, no cambiaremos el modelo ni cambiaremos las predicciones que obtendríamos para un valor dado de altura, número de calcetines, etc. En su lugar, haremos la siguiente pregunta: si mezclo aleatoriamente una sola columna de los datos de validación, dejando el objetivo y todas las demás columnas en su lugar, ¿cómo afectaría eso la precisión de las predicciones en esos datos ahora mezclados?.

Reordenar aleatoriamente una sola columna debería generar predicciones menos precisas, ya que los datos resultantes ya no corresponden a nada observado en el mundo real. La precisión del modelo se ve especialmente afectada si mezclamos una columna en la que el modelo se basó en gran medida para las predicciones. En este caso, cambiar la altura a los 10 años causaría predicciones terribles. Si en lugar de eso, barajáramos los calcetines que poseemos, las predicciones resultantes no sufrirían tanto. Con esta información, el proceso sería el siguiente:

• Consiguir un modelo entrenado,
• Mezclar los valores en una sola columna, hacer predicciones utilizando el conjunto de datos resultante. Utilizar estas predicciones y los valores objetivo reales para calcular cuánto sufrió la función de pérdida por la mezcla. Ese deterioro del rendimiento mide la importancia de la variable que se acaba de cambiar.
• Devolver los datos al orden original (deshaciendo la reproducción aleatoria del paso 2). Posteriormente se repite el paso 2 con la siguiente columna del conjunto de datos, hasta que haya calculado la importancia de cada columna.

Caso de Estudio

Nuestro ejemplo utilizará un modelo que predice si un equipo de fútbol ganador tendrá "el mejor jugador" según las estadísticas del equipo. El premio "Man of the Game" se otorga al mejor jugador del juego. La construcción de modelos no es el enfoque actual, por lo tanto se cargarán algunos datos y se creará un modelo rudimentario. Podrá descargar el conjunto de datos directamente desde nuestro repositorio haciendo clic aquí.

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree

import graphviz
import shap 
import eli5

from eli5.sklearn import PermutationImportance
from matplotlib import pyplot as plt
from pdpbox import pdp
from pdpbox import get_dataset
from pdpbox import info_plots

import os
os.environ["PATH"] += os.pathsep + 'C:/Program Files/Graphviz/bin'

data = pd.read_csv('fifa_2018_statistics.csv')

y = (data['Man of the Match'] == "Yes")  # Convertir de cadena "Sí" / "No" a binario
feature_names = [i for i in data.columns if data[i].dtype in [np.int64]]
X = data[feature_names]

train_X, val_X, train_y, val_y = train_test_split(X, y, random_state = 1)
my_model = RandomForestClassifier(n_estimators = 100, random_state = 0).fit(train_X, train_y)

• A continuación, se explica cómo calcular y mostrar importancias con la biblioteca eli5:

|

perm = PermutationImportance(my_model, random_state = 1).fit(val_X, val_y)
eli5.show_weights(perm, feature_names = val_X.columns.tolist())

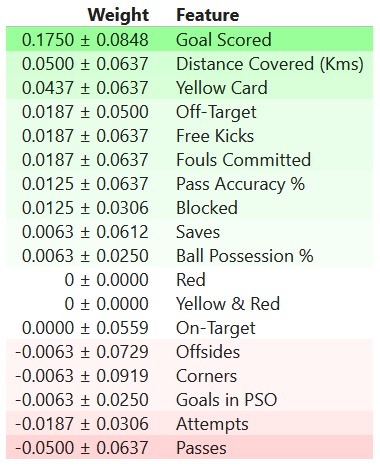
Interpretación de la importancia de la permutación

Los valores hacia la parte superior son las características más importantes, y aquellos hacia la parte inferior son los que menos importan. El primer número de cada fila muestra cuánto disminuyó el rendimiento del modelo con una mezcla aleatoria (en este caso, utilizando la "precisión" como métrica de rendimiento). Como la mayoría de las cosas en la ciencia de datos, existe cierta aleatoriedad en el cambio de rendimiento exacto al mezclar una columna. Medimos la cantidad de aleatoriedad en nuestro cálculo de la importancia de la permutación repitiendo el proceso con varias combinaciones. El número después de ± mide cómo varió el rendimiento de una reorganización a la siguiente.

Ocasionalmente verá valores negativos para la importancia de la permutación. En esos casos, las predicciones sobre los datos mezclados (o ruidosos) resultaron ser más precisas que los datos reales. Esto sucede cuando la función no importaba (debería haber tenido una importancia cercana a 0), pero la probabilidad aleatoria hizo que las predicciones en los datos mezclados fueran más precisas. Esto es más común con conjuntos de datos pequeños, como el de este ejemplo, porque hay más espacio para la suerte. En el ejemplo, la característica más importante fueron los goles marcados. Eso parece sensato. Los fanáticos del fútbol pueden tener cierta intuición sobre si el orden de otras variables es sorprendente o no.

Graficas de Dependencia Parcial

Si bien la importancia de la característica muestra qué variables afectan más a las predicciones, las gráficas de dependencia parcial muestran cómo una característica afecta las predicciones. Esto es útil para responder preguntas como:

• Controlando todas las demás características de la vivienda, ¿qué impacto tienen la longitud y la latitud en los precios de las viviendas?. Para reafirmar esto, ¿cómo se tasarían las casas de tamaño similar en diferentes áreas?,

• ¿Las diferencias de salud previstas entre dos grupos se deben a diferencias en sus dietas o se deben a algún otro factor?,

Si está familiarizado con los modelos de regresión lineal o logística, las gráficas de dependencia parcial se pueden interpretar de manera similar a los coeficientes de esos modelos. Sin embargo, las gráficas de dependencia parcial de modelos sofisticados pueden capturar patrones más complejos que los coeficientes de modelos simples. Si no está familiarizado con las regresiones lineales o logísticas, no se preocupe por esta comparación. Mostraremos un par de ejemplos, explicaremos la interpretación de estos gráficos y luego revisaremos el código para crearlos.

Funcionamiento

Al igual que la importancia de la permutación, las gráficas de dependencia parcial se calculan después de que se ha ajustado un modelo. El modelo se ajusta a datos reales que no han sido manipulados artificialmente de ninguna manera. En el ejemplo del fútbol, los equipos pueden diferir de muchas maneras. Cuántos pases hicieron, tiros que hicieron, goles que marcaron, etc. A primera vista, parece difícil desentrañar el efecto de estas características. Para ver cómo las gráficas parciales separan el efecto de cada característica, comenzamos considerando una sola fila de datos. Por ejemplo, esa fila de datos podría representar a un equipo que tuvo el balón el 50% del tiempo, realizó 100 pases, realizó 10 tiros y anotó 1 gol.

Usaremos el modelo ajustado para predecir el resultado (probabilidad de que el jugador ganara el "jugador más valioso"). Pero modificamos repetidamente el valor de una variable para hacer una serie de predicciones. Podríamos predecir el resultado si el equipo tuviera el balón solo el 40% del tiempo. Luego predecimos con ellos teniendo el balón el 50% del tiempo. Luego vuelva a predecir el 60%. Etcétera. Trazamos los resultados previstos (en el eje vertical) a medida que pasamos de valores pequeños de posesión de balón a valores grandes (en el eje horizontal). En esta descripción, usamos solo una fila de datos. Las interacciones entre entidades pueden hacer que el gráfico de una sola fila sea atípico. Entonces, repetimos ese experimento mental con múltiples filas del conjunto de datos original, y graficamos el resultado promedio predicho en el eje vertical. Vamos con el ejemplo.

train_X, val_X, train_y, val_y = train_test_split(X, y, random_state = 1)
tree_model = DecisionTreeClassifier(random_state = 0,
                                    max_depth = 5,
                                    min_samples_split = 5).fit(train_X, train_y)

• Nuestro primer ejemplo usa un árbol de decisiones, que puede ver a continuación. En la práctica, utilizará modelos más sofisticados para aplicaciones del mundo real.

tree_graph = tree.export_graphviz(tree_model, out_file = None, feature_names = feature_names)

graphviz.Source(tree_graph)

Como guía para leer el árbol:

• Las hojas con niños muestran su criterio de división en la parte superior.
• El par de valores en la parte inferior muestra el recuento de valores falsos y valores verdaderos para el objetivo, respectivamente, de puntos de datos en ese nodo del árbol.

Aquí está el código para crear la gráfica de dependencia parcial usando la biblioteca PDPBox.

pdp_goals = pdp.pdp_isolate(model = tree_model,
                            dataset = val_X,
                            model_features = feature_names,
                            feature = 'Goal Scored') # Crea los datos a trazar
pdp.pdp_plot(pdp_goals, 'Goal Scored')
plt.show()

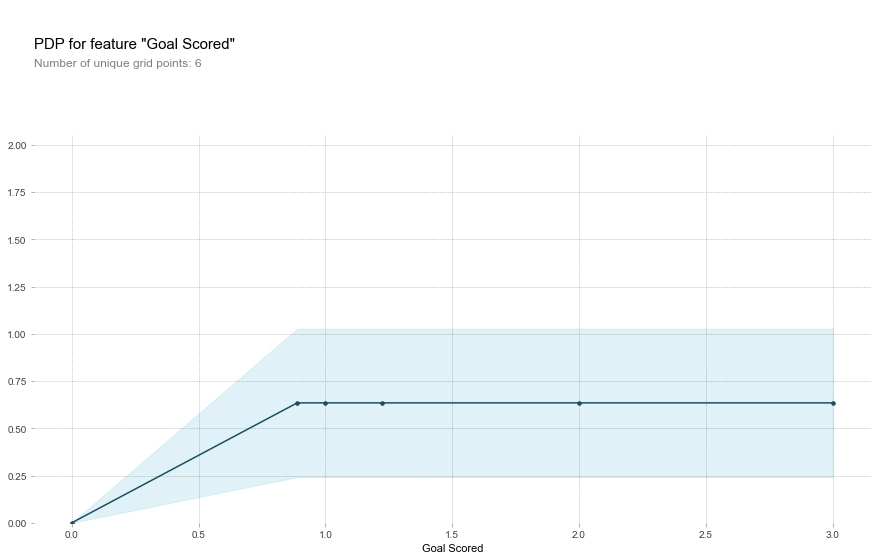
Vale la pena señalar algunos elementos al interpretar del gráfico anterior.

• El eje y se interpreta como un cambio en la predicción de lo que se predeciría en la línea de base o en el valor más a la izquierda.
• Un área sombreada en azul indica el nivel de confianza.

A partir de este gráfico en particular, vemos que marcar un gol aumenta sustancialmente sus posibilidades de ganar el premio de el "mejor jugador". Pero los objetivos adicionales más allá de eso parecen tener poco impacto en las predicciones.

Aquí hay otro diagrama de ejemplo:

feature_to_plot = 'Distance Covered (Kms)'

pdp_dist = pdp.pdp_isolate(model = tree_model,
                           dataset = val_X,
                           model_features = feature_names,
                           feature = feature_to_plot)
pdp.pdp_plot(pdp_dist, feature_to_plot)
plt.show()

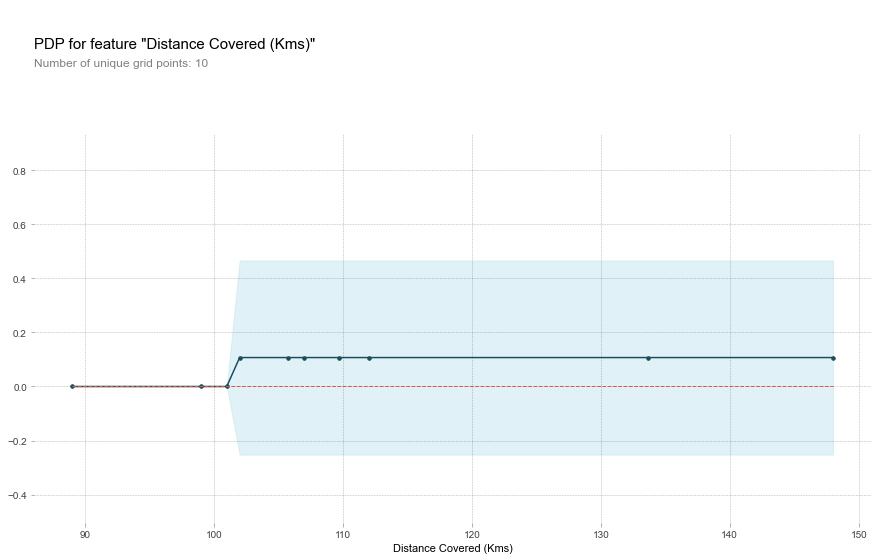
• Este gráfico parece demasiado simple para representar la realidad. Pero eso es porque el modelo es tan simple. Debería poder ver en el árbol de decisiones anterior que esto representa exactamente la estructura del modelo. Puede comparar fácilmente la estructura o las implicaciones de diferentes modelos. Aquí está el mismo gráfico con un modelo de bosque aleatorio.

rf_model = RandomForestClassifier(random_state = 0).fit(train_X, train_y) # Construye el modelo Random Forest

pdp_dist = pdp.pdp_isolate(model = rf_model,
                           dataset = val_X,
                           model_features = feature_names,
                           feature = feature_to_plot)
pdp.pdp_plot(pdp_dist, feature_to_plot)
plt.show()

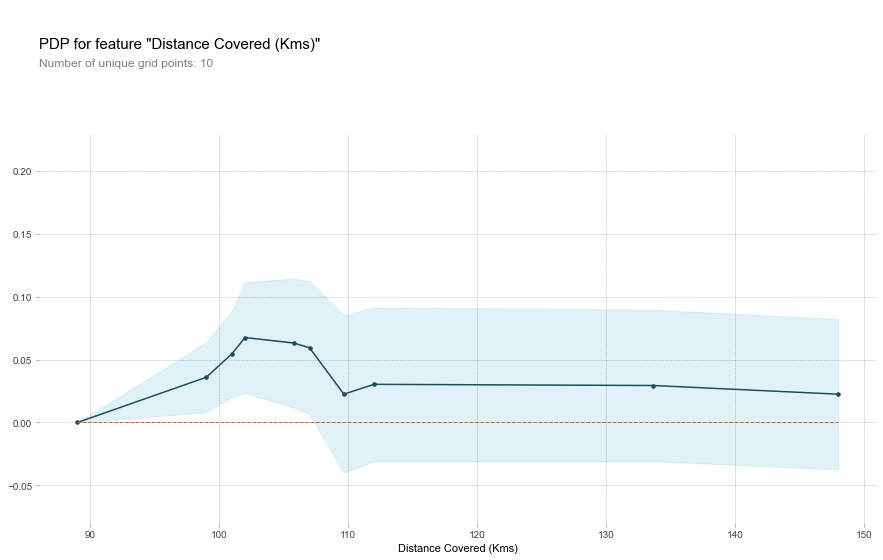
Este modelo muestra que es más probable ganar el premio del mejor jugador del partido si los jugadores corren un total de 100 km en el transcurso del juego. Aunque correr mucho más provoca predicciones más bajas. En general, la forma suave de esta curva parece más plausible que la función de paso del modelo de árbol de decisión. Aunque este conjunto de datos es lo suficientemente pequeño como para tener cuidado al interpretar cualquier modelo.

Gráficas de Dependencia Parcial 2D

Si tiene curiosidad acerca de las interacciones entre características, las gráficas de dependencia parcial 2D también son útiles. Un ejemplo puede aclarar esto. Usaremos nuevamente el modelo de árbol de decisión para este gráfico. Crearemos un gráfico extremadamente simple, pero deberíamos poder hacer coincidir lo que ve en el gráfico con el árbol en sí.

# Similar a la gráfica de PDP anterior, excepto que usamos pdp_interact en lugar de pdp_isolate y pdp_interact_plot en lugar de pdp_isolate_plot
features_to_plot = ['Goal Scored', 'Distance Covered (Kms)']

inter1  =  pdp.pdp_interact(model = tree_model,
                            dataset = val_X,
                            model_features = feature_names,
                            features = features_to_plot)
pdp.pdp_interact_plot(pdp_interact_out = inter1,
                      feature_names = features_to_plot,
                      plot_type = 'contour')
plt.show()

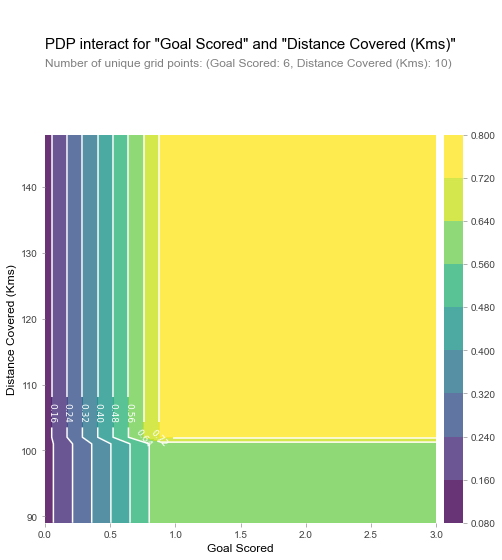
El gráfico anterior muestra predicciones para cualquier combinación de goles marcados y distancia recorrida. Por ejemplo, vemos las predicciones más altas cuando un equipo marca al menos 1 gol y corre una distancia total cercana a los 100 km. Si marca 0 goles, la distancia recorrida no importa. ¿Puedes ver esto rastreando el árbol de decisiones con 0 objetivos?. Pero la distancia puede afectar las predicciones si marcan goles. Asegurémonos de que podemos ver esto en la gráfica de dependencia parcial 2D. ¿Puedes ver este patrón también en el árbol de decisiones?.

Valores de Explicación de Aditivos Shapley (SHAP).

Hemos visto (y utilizado) técnicas para extraer información general de un modelo de aprendizaje automático. Pero, ¿qué sucede si desea desglosar cómo funciona el modelo para una predicción individual?. SHAP Values es un acrónimo de Shapley Additive Explanations, desglosa una predicción para mostrar el impacto de cada característica. ¿Dónde se puede usar esto?.

• Un modelo dice que un banco no debe prestarle dinero a alguien, y el banco está legalmente obligado a explicar la base de cada rechazo de préstamo.
• Un proveedor de atención médica desea identificar qué factores están impulsando el riesgo de cada paciente de padecer alguna enfermedad para poder abordar directamente esos factores de riesgo con intervenciones de salud específicas.

Para estos casos utilizarán los valores SHAP para explicar predicciones individuales en esta sección. En la siguiente sección, veremos cómo se pueden agregar información valiosa a nivel de modelo.

Funcionamiento

Los valores SHAP interpretan el impacto de tener un cierto valor para una característica determinada en comparación con la predicción que haríamos si esa característica tomara algún valor de referencia. Continuaremos con el ejemplo del fútbol a partir de los conocimientos aprendidos en la importancia de la permutación y los gráficos de dependencia parcial. En essos casos, se predijo si un equipo haría que un jugador ganara el premio al mejor jugador del Partido.

Entonces, podríamos preguntar:

• ¿Cuánto fue una predicción impulsada por el hecho de que el equipo marcó 3 goles?

Pero es más fácil dar una respuesta numérica concreta si reafirmamos esto como:

• Cuánto fue una predicción impulsada por el hecho de que el equipo marcó 3 goles, en lugar de una cantidad de goles de referencia.

Por supuesto, cada equipo tiene muchas características. Entonces, si respondemos a esta pregunta para el número de objetivos, podríamos repetir el proceso para todas las demás funciones. Los valores SHAP hacen esto de una manera que garantiza una propiedad agradable. Específicamente, descompone una predicción con la siguiente ecuación:

• sum(SHAP values for all features) = pred_for_team - pred_for_baseline_values

Es decir, los valores SHAP de todas las características se suman para explicar por qué mi predicción fue diferente de la línea de base. Esto nos permite descomponer una predicción en un gráfico el cual veremos más adelante.

¿Como se interpreta un gráfico de ese tipo?. Predijimos 0.7, mientras que base_value es 0.4979. Los valores de las características que provocan un aumento de las predicciones están en rosa y su tamaño visual muestra la magnitud del efecto de la característica. Los valores de las características que disminuyen la predicción están en azul. El mayor impacto proviene de que el gol anotado es 2. Aunque el valor de posesión del balón tiene un efecto significativo que disminuye la predicción.

Si resta la longitud de las barras azules de la longitud de las barras rosas, equivale a la distancia desde el valor base hasta la salida.

Existe cierta complejidad en la técnica, para garantizar que la línea de base más la suma de los efectos individuales se sumen a la predicción (que no es tan sencilla como parece). No entraremos en ese detalle aquí, ya que no es fundamental para usar la técnica. Esta publicación de blog tiene una explicación teórica más extensa.

Calculamos los valores de SHAP utilizando la maravillosa biblioteca Shap.

train_X, val_X, train_y, val_y = train_test_split(X, y, random_state = 1)
my_model = RandomForestClassifier(random_state = 0).fit(train_X, train_y)

Observaremos los valores de SHAP para una sola fila del conjunto de datos (elegimos arbitrariamente la fila 5). Para el contexto, veremos las predicciones sin procesar antes de ver los valores SHAP.

row_to_show = 5
data_for_prediction = val_X.iloc[row_to_show]  # use 1 fila de datos aquí. Podría usar varias filas si lo desea
data_for_prediction_array = data_for_prediction.values.reshape(1, -1)
my_model.predict_proba(data_for_prediction_array)

array([[0.29, 0.71]])

• El equipo tiene un 70% de probabilidades de que un jugador gane el premio. Ahora, pasaremos al código para obtener valores SHAP para esa única predicción.

explainer = shap.TreeExplainer(my_model) # Crea el objeto que pueda calcular valores Shap
shap_values = explainer.shap_values(data_for_prediction) # Calcula los valores de Shap

El objeto shap_values anterior es una lista con dos matrices. La primera matriz son los valores SHAP para un resultado negativo (no gane el premio), y la segunda matriz es la lista de valores SHAP para el resultado positivo (gana el premio). Por lo general, pensamos en las predicciones en términos de la predicción de un resultado positivo, por lo que sacaremos los valores SHAP para los resultados positivos (extrayendo shap_values). Es engorroso revisar matrices sin procesar, pero el paquete shap tiene una buena forma de visualizar los resultados.

shap.initjs()
shap.force_plot(explainer.expected_value[1], shap_values[1], data_for_prediction)

Visualization omitted, Javascript library not loaded!
Have you run `initjs()` in this notebook? If this notebook was from another user you must also trust this notebook (File -> Trust notebook). If you are viewing this notebook on github the Javascript has been stripped for security. If you are using JupyterLab this error is because a JupyterLab extension has not yet been written.

Si observa detenidamente el código donde creamos los valores SHAP, notará que hacemos referencia a Trees en shap.TreeExplainer(my_model). Pero el paquete SHAP tiene explicaciones para cada tipo de modelo.

• shap.DeepExplainer funciona con modelos de Deep Learning.
• shap.KernelExplainer funciona con todos los modelos, aunque es más lento que otros Explainers y ofrece una aproximación en lugar de valores exactos de Shap.

Aquí hay un ejemplo usando KernelExplainer para obtener resultados similares. Los resultados no son idénticos porque KernelExplainer da un resultado aproximado. Pero los resultados cuentan la misma historia.

k_explainer = shap.KernelExplainer(my_model.predict_proba, train_X) # utiliza Kernel SHAP para explicar las predicciones del conjunto de pruebas
k_shap_values = k_explainer.shap_values(data_for_prediction)
shap.force_plot(k_explainer.expected_value[1], k_shap_values[1], data_for_prediction)

Visualization omitted, Javascript library not loaded!
Have you run `initjs()` in this notebook? If this notebook was from another user you must also trust this notebook (File -> Trust notebook). If you are viewing this notebook on github the Javascript has been stripped for security. If you are using JupyterLab this error is because a JupyterLab extension has not yet been written.

Usos avanzados de los valores SHAP.

Comenzamos aprendiendo sobre la importancia de la permutación y las gráficas de dependencia parcial para obtener una descripción general de lo que ha aprendido el modelo. Luego aprendimos sobre los valores SHAP para desglosar los componentes de las predicciones individuales. Ahora ampliaremos los valores SHAP, viendo cómo la agregación de muchos valores SHAP puede brindar alternativas más detalladas a la importancia de la permutación y las gráficas de dependencia parcial.

Revisión de valores de SHAP

Los valores de Shap muestran cuánto cambió una característica dada nuestra predicción (en comparación con si hiciéramos esa predicción en algún valor de referencia de esa característica). Por ejemplo, considere un modelo ultra simple:

• y = 4 ∗ x1 + 2 ∗ x2

Si x1, toma el valor 2, en lugar de un valor de línea base de 0, entonces nuestro valor SHAP para x1. sería 8 (de 4 por 2). Estos son más difíciles de calcular con los modelos sofisticados que usamos en la práctica. Pero a través de un poco de inteligencia algorítmica, los valores de Shap nos permiten descomponer cualquier predicción en la suma de los efectos de cada valor de característica. Además de este buen desglose para cada predicción, la biblioteca Shap ofrece excelentes visualizaciones de grupos de valores Shap. Nos centraremos en dos de estas visualizaciones. Estas visualizaciones tienen similitudes conceptuales con la importancia de la permutación y las gráficas de dependencia parcial. Así que aquí se unirán varios hilos de los ejercicios anteriores.

Gráficos de resumen

La importancia de la permutación es excelente porque crea medidas numéricas simples para ver qué características son importantes para un modelo. Esto nos ayudó a hacer comparaciones entre características fácilmente, y puede presentar los gráficos resultantes a audiencias no técnicas. Pero no le dice qué importancia tiene cada característica. Si una característica tiene una importancia de permutación media, eso podría significar que tiene

• un gran efecto para algunas predicciones, pero ningún efecto en general, o
• Un efecto medio para todas las predicciones.

Los gráficos de resumen de SHAP nos brindan una vista panorámica de la importancia de las características y lo que las impulsa. Veremos un diagrama de ejemplo para los datos del fútbol.

Este gráfico está formado por muchos puntos. Cada punto tiene tres características:

• La ubicación vertical muestra qué característica está representando,
• El color muestra si esa característica fue alta o baja para esa fila del conjunto de datos,
• La ubicación horizontal muestra si el efecto de ese valor provocó una predicción mayor o menor.

Por ejemplo, el punto en la parte superior izquierda fue para un equipo que anotó pocos goles, reduciendo la predicción en 0,25. Algunas cosas que debería poder distinguir fácilmente:

• El modelo ignoró las características de rojo y amarillo y rojo,
• Por lo general, la tarjeta amarilla no afecta la predicción, pero hay un caso extremo en el que un valor alto provocó una predicción mucho más baja.
• Los valores altos de Goal anotado causaron predicciones más altas y los valores bajos causaron predicciones bajas.

Si busca el tiempo suficiente, hay mucha información en este gráfico. Te enfrentarás a algunas preguntas para probar cómo las lees en el ejercicio.

train_X, val_X, train_y, val_y = train_test_split(X, y, random_state = 1)
my_model = RandomForestClassifier(random_state = 0).fit(train_X, train_y)

• Obtenemos los valores SHAP para todos los datos de validación con el siguiente código. Es lo suficientemente breve como para que lo expliquemos en los comentarios.

explainer = shap.TreeExplainer(my_model) # Crear objeto que pueda calcular valores de shap
# calcula valores de shap. Esto es lo que se graficará.
# Calcula shap_values para todo val_X en lugar de una sola fila, para tener más datos para la gráfica.
shap_values = explainer.shap_values(val_X)
# Crea la trama. El índice de [1] se explica en el texto siguiente.
shap.summary_plot(shap_values[1], val_X)

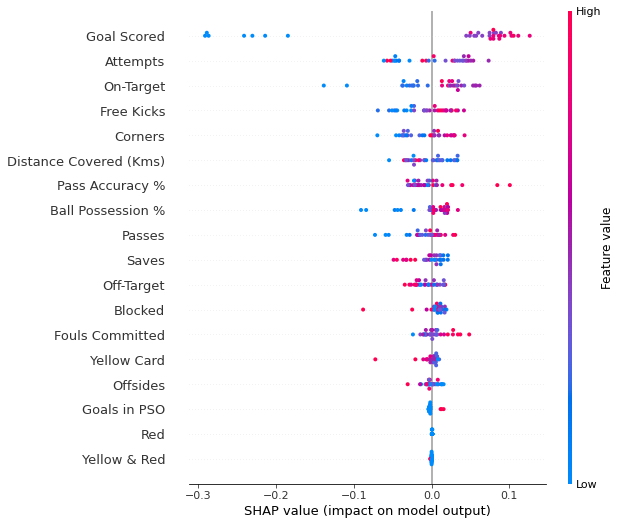
El código no es demasiado complicado. Pero hay algunas salvedades.

• Al graficar, llamamos shap_values. Para los problemas de clasificación, existe una matriz separada de valores SHAP para cada resultado posible. En este caso, indexamos para obtener los valores SHAP para la predicción de "Verdadero".
• El cálculo de los valores de SHAP puede resultar lento. No es un problema aquí, porque este conjunto de datos es pequeño. Pero querrá tener cuidado al ejecutarlos para trazar con conjuntos de datos de tamaño razonable. La excepción es cuando se usa un modelo xgboost, para el cual SHAP tiene algunas optimizaciones y, por lo tanto, es mucho más rápido.

Esto proporciona una excelente descripción general del modelo, pero es posible que deseemos profundizar en una sola característica. Ahí es donde entran en juego las parcelas de contribución de dependencia de SHAP.

Gráficos de Contribución de Dependencia de SHAP

Anteriormente, usamos Gráficos de dependencia parcial para mostrar cómo una sola característica impacta en las predicciones. Estos son reveladores y relevantes para muchos casos de uso del mundo real. Además, con un poco de esfuerzo, se pueden explicar a una audiencia no técnica. Pero hay muchas cosas que no muestran. Por ejemplo, ¿cuál es la distribución de efectos? ¿Es el efecto de tener un cierto valor bastante constante, o varía mucho dependiendo de los valores de otras características? Las gráficas de contribución de dependencia de SHAP brindan una perspectiva similar a las de los PDP, pero agregan muchos más detalles.

Empiece por centrarse en la forma y volveremos al color en un minuto. Cada punto representa una fila de datos. La ubicación horizontal es el valor real del conjunto de datos, y la ubicación vertical muestra lo que tuvo ese valor en la predicción. El hecho de que se incline hacia arriba indica que cuanto más posees la pelota, mayor es la predicción del modelo para ganar el premio al Hombre del Partido.

La extensión sugiere que otras características deben interactuar con el porcentaje de posesión de pelota. Por ejemplo, aquí hemos resaltado dos puntos con valores de posesión de balón similares. Ese valor hizo que una predicción aumentara y provocó que la otra disminuyera.

A modo de comparación, una regresión lineal simple produciría gráficos que son líneas perfectas, sin esta extensión. Esto sugiere que profundicemos en las interacciones, y los gráficos incluyen codificación de colores para ayudar a hacer eso. Si bien la tendencia principal es ascendente, puede inspeccionar visualmente si varía según el color de los puntos. Considere el siguiente ejemplo muy limitado de concreción.

Estos dos puntos se destacan espacialmente por estar alejados de la tendencia alcista. Ambos son de color violeta, lo que indica que el equipo anotó un gol. Puede interpretar esto como si dijera: En general, tener el balón aumenta las posibilidades de un equipo de que su jugador gane el premio. Pero si solo anotan un gol, esa tendencia se invierte y los jueces del premio pueden penalizarlos por tener tanto el balón si anotan tan poco. Fuera de esos pocos valores atípicos, la interacción indicada por el color no es muy dramática aquí. Pero a veces te llamará la atención.

Gráficos de Contribución de Dependencia en Código

Obtenemos la gráfica de contribución de dependencia con el siguiente código. La única línea que es diferente de summary_plot es la última línea.

explainer = shap.TreeExplainer(my_model) # Crear objeto que pueda calcular valores de shap
shap_values = explainer.shap_values(X) # calcular valores de shap. Esto es lo que se graficará.
shap.dependence_plot('Ball Possession %', shap_values[1], X, interaction_index="Goal Scored")

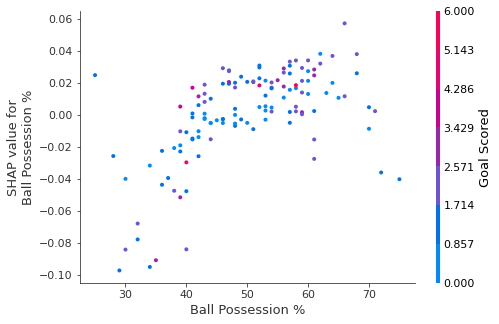
Si no proporciona un argumento para interactive_index, Shapley usa cierta lógica para elegir uno que pueda ser interesante. Esto no requirió escribir mucho código. Pero el truco con estas técnicas está en pensar críticamente sobre los resultados en lugar de escribir el código en sí.