Regresión Lineal con Scikit-learn.
Publicado el: 04 de Enero del 2021 - Jhonatan Montilla
Una de las maneras de predicción más antigua y básica es la regresión lineal, aún hoy día se utiliza ampliamente en muchos campos diferentes para extrapolar e interpolar datos. En este artículo, explicaremos los conceptos básicos de cómo y cuándo utilizarla con la ayuda de Scikit-learn de Python.
Carga de librerías
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.feature_selection import f_regression
- Comenzaremos con un conjunto de datos sencillo para probar un modelo de regresión lineal simple.
X=[[1],[2],[3],[4],[5],[6],[7],[8],[9]]
y=[1,2,3,4,5,6,7,8,9]
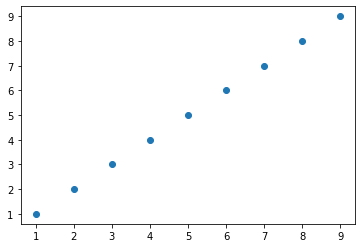
- Realizamos un gráfico de dispersión de los datos.
plt.scatter(X,y)
plt.show()
-
Lo datos del conjunto de datos son simétricos, x = y, por lo que será bastante sencillo para nuestro modelo de regresión predecir que el valor de la variable dependiente y para x (10) es 10.
-
Creamos el modelo de regrsión lineal a continuación.
model = linear_model.LinearRegression(fit_intercept = False)
model.fit(X,y)
LinearRegression(fit_intercept=False)
- En el código anterior primero se define el modelo de regresión lineal con la función linear_model.LinearRegression(), luego se ajusta el modelo con la función model.fit (x, y), ahora se procederá a revisar el coeficiente del modelo de regresión lineal.
model.coef_
array([1.])
-
El resultado es: 1. Significa que la ecuación del modelo de regresión lineal es: X = 1 * Y
-
Procederemos a realizar algunas predicciones con nuestro modelo de regresión lineal.
X_pred=[[10],[11],[12],[13],[14]]
model.predict(X_pred)
array([10., 11., 12., 13., 14.])
- Como era de esperar los resultados son lineales y proporcianeles a los valores de la variable independiente, esto se debe a que el coeficiente de la ecuación es 1
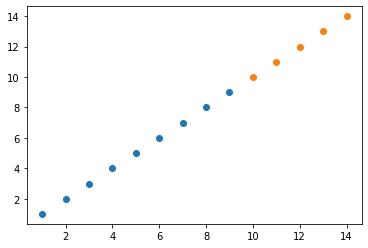
- Realizamos una gráfica de dispersión
plt.scatter(X,y)
plt.scatter(X_pred,model.predict(X_pred))
plt.show()
-
Un resultado completamente esperado una secuencia de puntos que describen una trayectoria con ángulo de 45°
-
Ahora, se procederá a realizar un modelo de regresión lineal de dos dimensiones.
# 1. Conjunto de datos
X=[[11],[12],[13],[14],[15],[16],[17],[18],[19]]
y=[1,2,3,4,5,6,7,8,9]
# 2. Definir y ajustar el modelo
model=linear_model.LinearRegression(fit_intercept=False)
model.fit(X,y)
print("Coeficiente: ",model.coef_, "\n")
# 3. Obtener predicciones
X_pred=np.arange(1,25).reshape(-1,1)
y_pred=model.predict(X_pred)
# 4. Visualización (valores del conjunto de datos vs predicciones)
plt.scatter(X,y)
plt.scatter(X_pred,y_pred)
plt.show()
Coeficiente: [0.35251799]
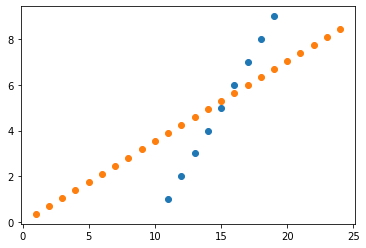
-
Parece que el modelo de regresión lineal anterior no está funcionando adecuadamente, esto se debe a que falta una parte crucial de la ecuación del modelo de regresión lineal. ¡La intercepción!
-
La intersección es un valor constante que se suma a la ecuación independientemente de los valores de las variables, para esto será necesario eliminar "fit_intercept = False" y se prueba nuevamente.
Y = intersección + coeficiente X Y = (-10) + (1 X)
# Se define y se ajusta el modelo
model=linear_model.LinearRegression()
model.fit(X,y)
print("\nIntersección: ",model.intercept_)
print("\nCoeficiente: ", model.coef_, "\n")
# Obtener predicicones
X_pred=np.arange(1,25).reshape(-1,1)
y_pred=model.predict(X_pred)
# Visualización
plt.scatter(X_pred,y_pred, color='orange')
plt.scatter(X,y)
plt.show()
Intersección: -10.000000000000004 Coeficiente: [1.]
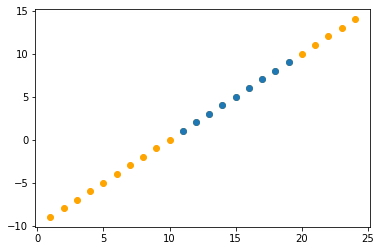
- Funciona correctamente, de esta manera se ejecuta una regresión lineal básica.
Análisis del modelo de regresión lineal.¶
El tipo de regresión utilizada anteriormente es la de los Mínimos Cuadrados Ordinarios (MCO). La manera en que este modelo evalúa los resultados a menudo se conoce como métricas, buscando la suma residual de cuadrados. El residual es simplemente la diferencia entre el valor predicho por el modelo y el valor real.
- Veamos otro ejemplo.
# Conjunto de datos
X=[[1],[2],[3],[4],[5],[6],[7],[8],[9]]
y=[1,2,3,4,5,6,7,8,9]
# Crea y ajusta el modelo de regresión lineal
model = linear_model.LinearRegression(fit_intercept=False)
model.fit(X,y)
# Predicciones del modelo
X_pred = [[10],[11],[12],[13],[14]]
y_true = X_pred
y_pred = model.predict(X_pred)
# Cálculo del Error Cuadrático Medio (MSE)
print('Error: %.2f' % mean_squared_error(X_pred, y_pred))
# Coeficioente de determinación: 1 será una predicción perfecta
print('Coeficiente: %.2f' % r2_score(y_true, y_pred))
Error: 0.00 Coeficiente: 1.00
-
No existen residuos en esta regresión, por lo tanto el error cuadrático medio es cero.
-
R2 es el coeficiente de determinación, donde una puntuación perfecta sería 1, disminuyendo a medida que los puntos predichos se alejan de los valores reales.
-
A continuación se evaluarán varios coeficientes de determinación con diferentes predicciones.
# Predicciones 1
y_true = [1, 2, 3]
y_pred = [1, 2, 3]
print('Coeficiente de determinación: %.2f' % r2_score(y_true, y_pred))
# Predicciones 2
y_true = [1, 2, 3]
y_pred = [1.1, 2.1, 3.1]
print('Coeficiente de determinación: %.2f' % r2_score(y_true, y_pred))
# Predicciones 3
y_true = [1, 2, 3]
y_pred = [3, 2, 1]
print('Coeficiente de determinación: %.2f' % r2_score(y_true, y_pred))
Coeficiente de determinación: 1.00 Coeficiente de determinación: 0.98 Coeficiente de determinación: -3.00
-
Hasta los momentos hemos visto cómo construir un modelo de regresión lineal simple, cómo ajustar los datos a este, extrapolar conclusiones y las métricas a usar para comparar los modelos.
-
Ahora, veremos algo de bastante importancia. ¡Los supuestos!. Las suposiciones son como requisitos previos; tenemos que comprobar para saber si este método funcionará en nuestros datos. no incluir los supuestos o ejecutar un modelo de regresión lineal independientemente de estos puede afectarlo de manera negativa, reduciendo su presición, es recomedable realizar más investigaciones sobre las suposiciones si se va a confiar mucho en los resultados a obtener del modelo, tal como se recomienda para cualquier modelo estadístico.
-
Linealidad: esto significa que la relación entre las dos variables debe ser lineal.
-
Independencia: las observaciones deben ser independientes entre sí. La cantidad de lluvia diaria no depende de cuánto llovió el día siguiente o el anterior, pero la cantidad de agua en un depósito depende en gran medida de sus valores anteriores.
-
Homoscedasticidad: esto significa que los residuos deben tener una varianza constante. Las series de tiempo suelen tener problemas con esto. Inicialmente, se obtienen predicciones consistentes, sin embargo, el error aumenta a medida que avanza en el tiempo.
-
Normalidad: los errores deben distribuirse normalmente. En este caso, se deben buscar desviaciones significativas de una distribución normal, como una distribución de error muy sesgada hacia la derecha o hacia la izquierda.
-
Tamaño de la muestra: la muestra debe tener al menos 20 observaciones.
Ahora se utilizaremos un modelo MCO con múltiples variables explicativas. Es importante recordar que las variables explicativas deben ser independientes entre sí.
Se creará un conjunto de datos con algunos datos aleatorios y ficticios para una tienda de batidos.
# Crea el conjunto de datos
df = pd.DataFrame(np.arange(0, 10))
# Se cargan los datos ficticios aleatórios
df['ventas'] = [100, 120, 115, 150, 175, 180, 200, 230, 230, 250]
df['temperatura'] = [20, 22, 21, 26, 28, 30, 32, 34, 36, 38]
df['prob_lluvia'] = [0.85, 0.6, 0.8, 0.6, 0.55, 0.53, 0.4, 0.35, 0.5, 0.18]
df['precio_accion'] = [39.8, 39.8, 41.8, 46.8, 39.11, 37.86, 35.7, 35.9, 39.1, 42]
# Visualiza el conjunto de datos
df.head()
| 0 | ventas | temperatura | prob_lluvia | precio_accion | |
|---|---|---|---|---|---|
| 0 | 0 | 100 | 20 | 0.85 | 39.80 |
| 1 | 1 | 120 | 22 | 0.60 | 39.80 |
| 2 | 2 | 115 | 21 | 0.80 | 41.80 |
| 3 | 3 | 150 | 26 | 0.60 | 46.80 |
| 4 | 4 | 175 | 28 | 0.55 | 39.11 |
# Gráficos de dispersión de las variables, temperatura,
# probabilidad de lluvia, y precio de la acción según
# las ventas
fig, ax = plt.subplots(3, figsize=(16,8))
ax = plt.subplot(221)
ax.scatter(df['ventas'], df['temperatura'])
ax = plt.subplot(222)
ax.scatter(df['ventas'], df['prob_lluvia'])
ax = plt.subplot(223)
ax.scatter(df['ventas'], df['precio_accion'])
plt.show()

Con las tres variables se pretende predecir las ventas de batidos, a través de la temperatura, la probabilidad de que llueva ese día y el valor de cierre diario del precio de las acciones de Microsoft. Quizás, la última no es la mejor opción para ayudarnos a predecir las ventas de batidos. Existen varias maneras de comprobar si una variable ayuda a predecir el resultado de otra. Este método se denomina Selección de Características.
El método más utilizado es verificar el valor p, el valor p indica la probabilidad de encontrar valores tan extremos como los observados en los valores de pruebas. por lo tanto, los coeficientes son una medida de la relación entre dos variables, y el valor p de los coeficientes es una medida de la significancia estadística.
Se entenderá mejor este concepto a través del siguiente ejemplo.
F, pval = f_regression(df[['precio_accion','prob_lluvia','temperatura']], df['ventas'])
print('precio_accion: %.8f' % pval[0],'\nprob_lluvia: %.8f' % pval[1], '\ntemperatura: %.8f' % pval[2])
precio_accion: 0.36620290 prob_lluvia: 0.00020982 temperatura: 0.00000000
Haciendo uso de la clase f_regression() de ScikitLearn, feature_selection. Este método devuelve los valores F y los valores p, por ahora, se analizarán los valores p, buscando relaciones con una significancia estadística igual o superior al 95%, en otras palabras, un valor p inferior al 5%. Como se puede observar ver en los resultados, el precio de las acciones de Microsoft no es una variable útil para predecir las ventas de batidos.
A continuación el ejemplo completo.
# Ajusta el modelo, se obtiene la intercepción y el coeficiente
model.fit(df[['prob_lluvia', 'temperatura',]], df['ventas'])
print('Intercepción: ', model.intercept_)
print('Coeficiente: ', model.coef_)
# Se muestra la ecuación del modelo de regresión lineal
print('\nVentas = %.2f' % model.intercept_, '+ (%.2f' % model.coef_[0], '* Probabilidad de Lluvia) + (%.2f' % model.coef_[1], ' * Temperatura)')
# Obtiene predicciones
y_pred = model.predict(df[['prob_lluvia','temperatura']])
# Calcula el Error Cuadrático Medio (MSE)
print('\nError (MSE): %.2f' % mean_squared_error(df['ventas'],y_pred))
# Calcula el Coeficiente de Determinación
print('Coeficiente de Determinación: %.2f' % r2_score(df['ventas'],y_pred))
# Representación gráfica del modelo de regresión lineal
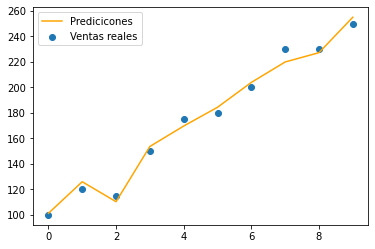
plt.plot(df.index, y_pred, color='orange')
plt.scatter(df.index, df['ventas'])
plt.legend(['Predicicones', 'Ventas reales'])
plt.show()
Intercepción: 0.0 Coeficiente: [-43.55818331 6.91493153] Ventas = 0.00 + (-43.56 * Probabilidad de Lluvia) + (6.91 * Temperatura) Error (MSE): 26.99 Coeficiente de Determinación: 0.99
print('Predicción: %.0f' % model.predict([[0.1, 27]]))
Predicción: 182
- Si mañana el pronóstico del clima indica una temperatura de 27°C con un 10% de probabilidad de lluvia, según el modelo de regresión lineal se estima vender alrededor de 182 batidos.
Ventas = 0.00 + (-43.56 x 0.1) + (6.91 x 27)
Ventas = -4.37 + 186.57
Ventas = ~182
-
Existen diferentes métodos de selección de funciones, métricas, y suposiciones que permiten verificar los datos, métodos de validación cruzada y mucho más.
-
Esperamos que este resumen sobre regresión lineal le haya ayudado a entender los conceptos básicos para desarrollar más conocimientos sobre este interesante tema.