Volver al Inicio

• Anterior
• Siguiente

Modelo de Aprendizaje Automático (ML)

Publicado el: 06 de Enero del 2021 - Jhonatan Montilla

En este artículo se creará un modelo de aprendizaje automático simple, usando un conjunto de datos para predecir el tamaño de la tripulación de un barco, este proyecto está organizado de la siguiente manera:

1. Procesamiento de datos y selección de variables,
2. Creación del Modelo de Regresión Lineal Múltiple,
3. Ajuste de Hiperparámetros y,
4. Técnicas para la Reducción de Dimensionalidad.

Podrá descargar el conjunto de datos haciendo clic en el enlace directo a nuestro repositorio.

Seguidamente se cargan todas las librerías necesarias.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import LabelEncoder,OneHotEncoder
from sklearn.compose import ColumnTransformer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Lasso
from sklearn.decomposition import PCA
from sklearn.pipeline import Pipeline

1. Procesamiento de datos y selección de variables

Lectura del conjunto de datos

df=pd.read_csv("cruise_ship_info.csv")

df.head()

	Ship_name	Cruise_line	Age	Tonnage	passengers	length	cabins	passenger_density	crew
0	Journey	Azamara	6	30.277	6.94	5.94	3.55	42.64	3.55
1	Quest	Azamara	6	30.277	6.94	5.94	3.55	42.64	3.55
2	Celebration	Carnival	26	47.262	14.86	7.22	7.43	31.80	6.70
3	Conquest	Carnival	11	110.000	29.74	9.53	14.88	36.99	19.10
4	Destiny	Carnival	17	101.353	26.42	8.92	13.21	38.36	10.00

Cálculo de estadísticas básicas de los datos.

df.describe()

	Age	Tonnage	passengers	length	cabins	passenger_density	crew
count	158.000000	158.000000	158.000000	158.000000	158.000000	158.000000	158.000000
mean	15.689873	71.284671	18.457405	8.130633	8.830000	39.900949	7.794177
std	7.615691	37.229540	9.677095	1.793474	4.471417	8.639217	3.503487
min	4.000000	2.329000	0.660000	2.790000	0.330000	17.700000	0.590000
25%	10.000000	46.013000	12.535000	7.100000	6.132500	34.570000	5.480000
50%	14.000000	71.899000	19.500000	8.555000	9.570000	39.085000	8.150000
75%	20.000000	90.772500	24.845000	9.510000	10.885000	44.185000	9.990000
max	48.000000	220.000000	54.000000	11.820000	27.000000	71.430000	21.000000

cols = ['Age', 'Tonnage', 'passengers', 'length', 'cabins','passenger_density','crew']

sns.pairplot(df[cols], height=2.0);

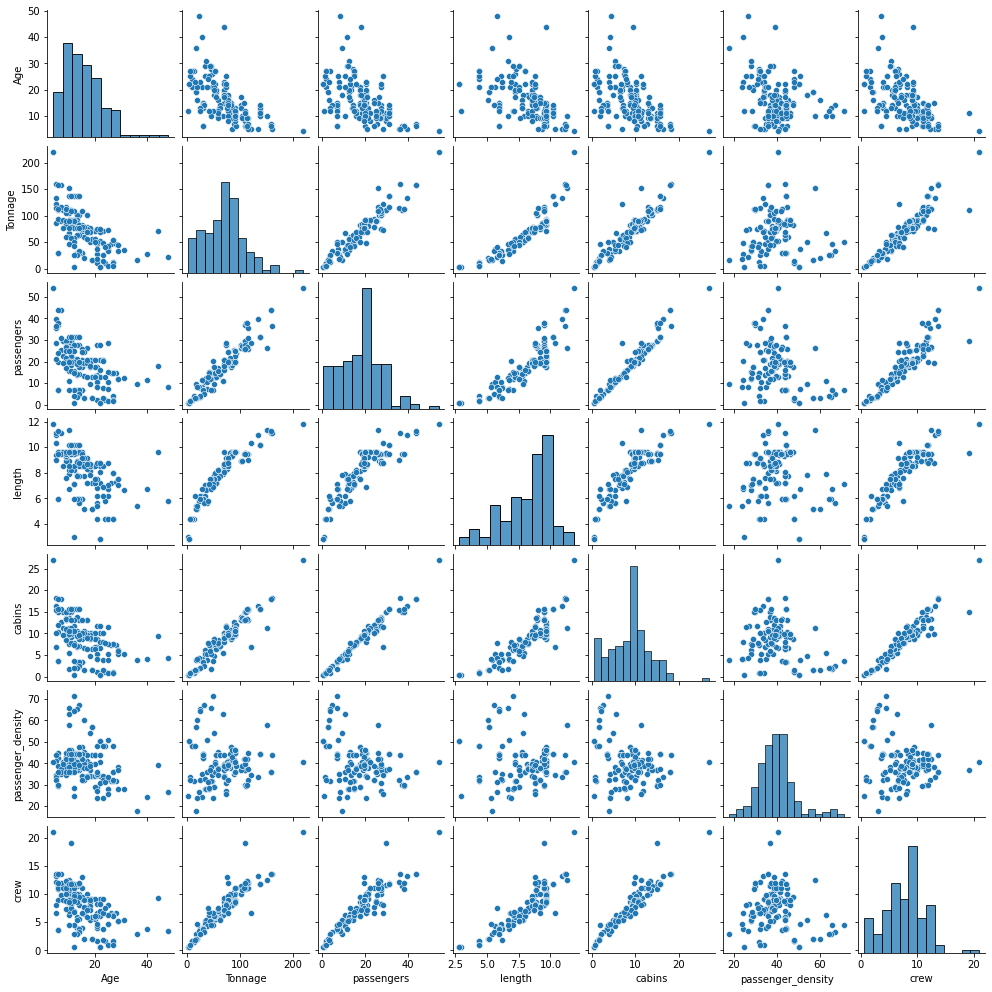
• Se puede observar que las variables están en diferentes escalas, para la muestra la variable Edad varía de aproximadamente 16 años a 48 años, mientras que la variable Tonelaje varía de 2 a 220, ver gráficos de densidad de probabilidad a continuación. Por lo tanto, es importante que cuando se construye un modelo de regresión usando estas variables, las variables tengan a la misma escala, estandarizando o normalizando los datos.

• Se puede observar que la variable objetivo "Tripulación" se correlaciona bien con 4 variables predictoras, "Tonelaje", "Pasajeros", "Longitud" y "Cabinas".

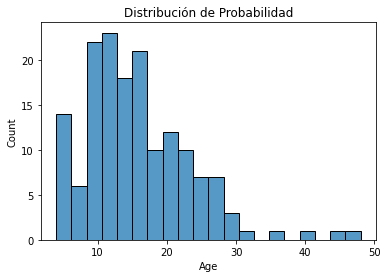
sns.histplot(df['Age'],bins=20)
plt.title("Distribución de Probabilidad")
plt.show()

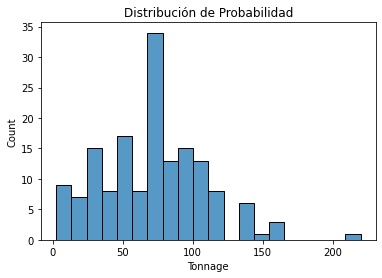
sns.histplot(df['Tonnage'],bins=20)
plt.title("Distribución de Probabilidad")
plt.show()

Selección de Variable Objetivo "Tripulación"

• Cálculo de la matriz de covarianza

cols = ['Age', 'Tonnage', 'passengers', 'length', 'cabins','passenger_density','crew']
stdsc = StandardScaler()
X_std = stdsc.fit_transform(df[cols].iloc[:,range(0,7)].values)

cov_mat =np.cov(X_std.T)
plt.figure(figsize=(10,10))
sns.set(font_scale=1.5)
hm = sns.heatmap(cov_mat,
                 cbar=True,
                 annot=True,
                 square=True,
                 fmt='.2f',
                 annot_kws={'size': 12},
                 yticklabels=cols,
                 xticklabels=cols)
plt.title("Matriz de Covarianza de \nCoeficientes de Correlación \n")
plt.tight_layout()
plt.show()

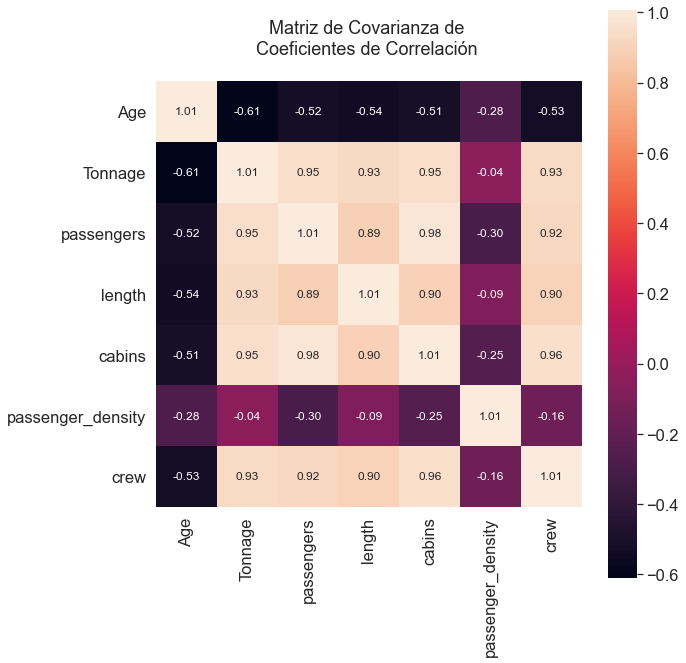
Selección de Variables Significativas

En la gráfica de matriz de covarianza anterior se puede observar que la variable "Tripulación" se correlaciona fuertemente con 4 variables predictoras: "Tonelaje", "Pasajeros", "Longitud y "Cabinas"

cols_selected = ['Tonnage', 'passengers', 'length', 'cabins','crew']

df[cols_selected].head()

	Tonnage	passengers	length	cabins	crew
0	30.277	6.94	5.94	3.55	3.55
1	30.277	6.94	5.94	3.55	3.55
2	47.262	14.86	7.22	7.43	6.70
3	110.000	29.74	9.53	14.88	19.10
4	101.353	26.42	8.92	13.21	10.00

X = df[cols_selected].iloc[:,0:4].values    # matriz de características 
y = df[cols_selected]['crew'].values        # variable de destino

X.shape

(158, 4)

y.shape

(158,)

Codificación de Variables Categóricas (One-Hot Encoder)

• Para la realización de la codificación se requieren crear variables de tipo dummies (complementarias) que contengan las categorías de cada variable como se muestra a continuación.

ohe = ColumnTransformer([('encoder', OneHotEncoder(), [0])],
                        remainder='passthrough')

df2 = pd.get_dummies(df[['Ship_name', 'Cruise_line','Age', 'Tonnage', 'passengers', 'length', 'cabins','passenger_density','crew']])  

df2.head()

	Age	Tonnage	passengers	length	cabins	passenger_density	crew	Ship_name_Adventure	Ship_name_Allegra	Ship_name_Amsterdam	...	Cruise_line_Oceania	Cruise_line_Orient	Cruise_line_P&O	Cruise_line_Princess	Cruise_line_Regent_Seven_Seas	Cruise_line_Royal_Caribbean	Cruise_line_Seabourn	Cruise_line_Silversea	Cruise_line_Star	Cruise_line_Windstar
0	6	30.277	6.94	5.94	3.55	42.64	3.55	0	0	0	...	0	0	0	0	0	0	0	0	0	0
1	6	30.277	6.94	5.94	3.55	42.64	3.55	0	0	0	...	0	0	0	0	0	0	0	0	0	0
2	26	47.262	14.86	7.22	7.43	31.80	6.70	0	0	0	...	0	0	0	0	0	0	0	0	0	0
3	11	110.000	29.74	9.53	14.88	36.99	19.10	0	0	0	...	0	0	0	0	0	0	0	0	0	0
4	17	101.353	26.42	8.92	13.21	38.36	10.00	0	0	0	...	0	0	0	0	0	0	0	0	0	0

5 rows × 165 columns

plt.scatter(df2['Ship_name_Adventure'],df2['crew'])
plt.xlabel('Nombre del Barco')
plt.ylabel('Tripulación')
plt.show()

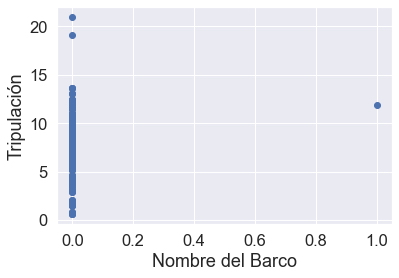
• Para la construcción de un modelo de regresión simplificado, nos enfocaremos únicamente en las características ordinales, no se utilizarán las funciones categóricas "Ship_name" ni "Cruise_line", es decir, construiremos un modelo simple usando solo 4 características ordinales "Tonelaje", "Pasajeros", "Longitud y "Cabinas".

Partición de los datos en los conjuntos de Prueba y Entrenamiento

X = df[cols_selected].iloc[:,0:4].values
y = df[cols_selected]['crew']

X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.4, random_state=0)

2. Construcción del Modelo de Regresión Múltiple

El modelo de regresión múltiple de Aprendizaje Automático (ML) para predecir el tamaño de la "Tripulación" de un barco se puede expresar como:

$$ \hat{y}_{i} = w_0 + \sum_{j=1}^{4} X_{ij} w_j $$

slr = LinearRegression()
slr.fit(X_train, y_train)
y_train_pred = slr.predict(X_train)
y_test_pred = slr.predict(X_test)

plt.scatter(y_train_pred,  y_train_pred - y_train,
            c='steelblue', marker='o', edgecolor='white',
            label='Datos de entrenamiento')
plt.scatter(y_test_pred,  y_test_pred - y_test,
            c='limegreen', marker='s', edgecolor='white',
            label='Datos de prueba')
plt.xlabel('Valores predichos')
plt.ylabel('Residuos')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=150, color='gray', lw=1)
plt.xlim([-10, 90])
plt.tight_layout()
plt.legend(loc='lower right')
plt.show()

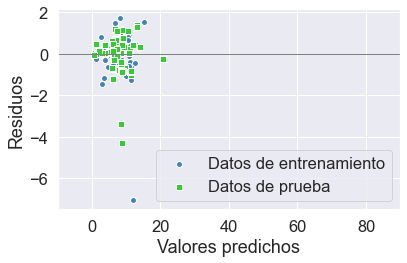
Evaluación del Modelo de Regresión

print('MSE train: %.3f, test: %.3f' % (
        mean_squared_error(y_train, y_train_pred),
        mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (
        r2_score(y_train, y_train_pred),
        r2_score(y_test, y_test_pred)))

MSE train: 0.955, test: 0.889
R^2 train: 0.920, test: 0.928

Revisión de los Coeficientes de Regresión

slr.fit(X_train, y_train).intercept_

-0.7525074496158375

slr.fit(X_train, y_train).coef_

array([ 0.01902703, -0.15001099,  0.37876395,  0.77613801])

3. Ajuste de Hiperparámetros

• Estandarización de funciones, y validación cruzada.

X = df[cols_selected].iloc[:,0:4].values     
y = df[cols_selected]['crew']  
sc_y = StandardScaler()
sc_x = StandardScaler()
y_std = sc_y.fit_transform(y_train[:, np.newaxis]).flatten()

train_score = []
test_score = []

for i in range(10):
    X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.4, random_state=i)
    y_train_std = sc_y.fit_transform(y_train[:, np.newaxis]).flatten()
    pipe_lr = Pipeline([('scl', StandardScaler()),('pca', PCA(n_components=4)),('slr', LinearRegression())])
    pipe_lr.fit(X_train, y_train_std)
    y_train_pred_std=pipe_lr.predict(X_train)
    y_test_pred_std=pipe_lr.predict(X_test)
    y_train_pred=sc_y.inverse_transform(y_train_pred_std)
    y_test_pred=sc_y.inverse_transform(y_test_pred_std)
    train_score = np.append(train_score, r2_score(y_train, y_train_pred))
    test_score = np.append(test_score, r2_score(y_test, y_test_pred))

train_score

array([0.92028261, 0.91733937, 0.94839385, 0.93899476, 0.90621451,
       0.91156903, 0.92726066, 0.94000795, 0.93922948, 0.93629554])

test_score

array([0.92827978, 0.93807946, 0.8741834 , 0.89901199, 0.94781315,
       0.91880183, 0.91437408, 0.89660876, 0.90427477, 0.90139208])

print('R2 train: %.3f +/- %.3f' % (np.mean(train_score),np.std(train_score)))

R2 train: 0.929 +/- 0.013

print('R2 test: %.3f +/- %.3f' % (np.mean(test_score),np.std(test_score)))

R2 test: 0.912 +/- 0.021

4. Técnicas de Reducción de Dimensionalidad del Modelo

Análisis de Componentes Principales (PCA)

train_score = []
test_score = []
cum_variance = []

for i in range(1,5):
    X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.4, random_state=0)
    y_train_std = sc_y.fit_transform(y_train[:, np.newaxis]).flatten()
    pipe_lr = Pipeline([('scl', StandardScaler()),('pca', PCA(n_components=i)),('slr', LinearRegression())])
    pipe_lr.fit(X_train, y_train_std)
    y_train_pred_std=pipe_lr.predict(X_train)
    y_test_pred_std=pipe_lr.predict(X_test)
    y_train_pred=sc_y.inverse_transform(y_train_pred_std)
    y_test_pred=sc_y.inverse_transform(y_test_pred_std)
    train_score = np.append(train_score, r2_score(y_train, y_train_pred))
    test_score = np.append(test_score, r2_score(y_test, y_test_pred))
    cum_variance = np.append(cum_variance, np.sum(pipe_lr.fit(X_train, y_train).named_steps['pca'].explained_variance_ratio_))

train_score

array([0.90411898, 0.9041488 , 0.90416405, 0.92028261])

test_score

array([0.89217843, 0.89174896, 0.89159266, 0.92827978])

cum_variance

array([0.949817  , 0.98322819, 0.99587366, 1.        ])

plt.scatter(cum_variance,train_score, label = "Entrenamiento")
plt.plot(cum_variance, train_score)
plt.scatter(cum_variance,test_score, label = "Prueba")
plt.plot(cum_variance, test_score)
plt.xlabel("Varianza Acumulada")
plt.ylabel("R2")
plt.legend()
plt.show()

Análisis

Se puede observar que al aumentar el número de componentes principales de 1 a 4, los puntajes de entrenamiento y pruebas mejoran, esto se debe a que con menos componentes, hay un mayor sesgo de error en el modelo debido a que el modelo se encuentra demasiado simplificado, a medida que se aumenta el número de componentes principales, el error de sesgo se reduce pero, se aumenta la complejidad del modelo.

Regresión Regularizada: Lazo

• Esta es otra técnica de reducción de dimensionalidad

X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.4, random_state=0)
y_train_std = sc_y.fit_transform(y_train[:, np.newaxis]).flatten()
X_train_std = sc_x.fit_transform(X_train)
X_test_std = sc_x.transform(X_test)

alpha = np.linspace(0.01,0.4,10)

lasso = Lasso(alpha=0.7)
r2_train=[]
r2_test=[]
norm = []
for i in range(10):
    lasso = Lasso(alpha=alpha[i])
    lasso.fit(X_train_std,y_train_std)
    y_train_std=lasso.predict(X_train_std)
    y_test_std=lasso.predict(X_test_std)
    r2_train=np.append(r2_train,r2_score(y_train,sc_y.inverse_transform(y_train_std)))
    r2_test=np.append(r2_test,r2_score(y_test,sc_y.inverse_transform(y_test_std)))
    norm= np.append(norm,np.linalg.norm(lasso.coef_))

plt.scatter(alpha,r2_train,label="Entrenamiento")
plt.plot(alpha,r2_train)
plt.scatter(alpha,r2_test,label="Pruebas")
plt.plot(alpha,r2_test)
plt.scatter(alpha,norm,label = "Normal")
plt.plot(alpha,norm)
plt.ylim(-0.1,1)
plt.xlim(0,.43)
plt.xlabel("Alpha")
plt.ylabel("R2")
plt.legend()
plt.show()

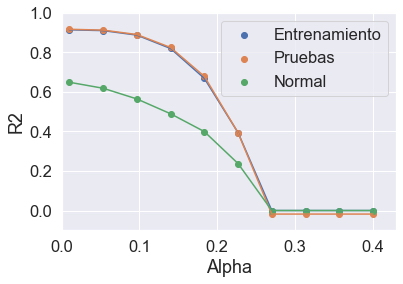
Anñalisis

Se puede observar que a medida que aumenta el parámetro de regularización $ \ alpha $, la norma de los coeficientes de regresión se vuelve cada vez más pequeña. Esto significa que más coeficientes de regresión tienden a cero, lo que pretende aumentar el error de sesgo (sobre simplificación). El mejor valor para equilibrar la compensación sesgo-varianza es cuando $ \ alpha $ se mantiene bajo, es decir $ \ alpha = 0.1 $ o menos.