Volver al Inicio
Volver al Inicio
 Volver al Inicio
Volver al Inicio
02 de Junio del 2022 | Jhonatan Montilla
Los datos son el combustible en los proyectos de Data Science. Pero, ¿y si las observaciones son escasas, caras o difíciles de medir? Los datos sintéticos pueden ser la solución. Los datos sintéticos son datos generados artificialmente que imitan las propiedades estadísticas de los eventos del mundo real. Demostraré cómo crear datos sintéticos continuos mediante el muestreo de distribuciones univariadas. Primero, mostraré cómo evaluar sistemas y procesos por simulación donde necesitamos elegir una distribución de probabilidad y especificar los parámetros. En segundo lugar, demostraré cómo generar muestras que imiten las propiedades de un conjunto de datos existente, es decir, las variables aleatorias que se distribuyen de acuerdo con un modelo probabilístico. Todos los ejemplos se crean utilizando scipy y la biblioteca distfit.
Si encuentra útil este artículo, use mi enlace de referencia para continuar aprendiendo sin límites y regístrese para obtener una membresía de Medium. ¡Además, sígueme para estar al día con mi contenido más reciente!
En la última década, la cantidad de datos ha crecido rápidamente y ha dado lugar a la idea de que los datos de mayor calidad son más importantes que la cantidad. Una mayor calidad puede ayudar a sacar conclusiones más precisas y decisiones mejor informadas. Hay muchas organizaciones y dominios donde los datos sintéticos pueden ser útiles, pero hay uno en particular que está fuertemente invertido en datos sintéticos, a saber, para vehículos autónomos. Aquí, los datos se generan para muchos casos extremos que posteriormente se utilizan para entrenar modelos. Empresas como Gartner subrayan la importancia de los datos sintéticos, y predicen que los datos reales se verán eclipsados muy pronto [1]. Ejemplos claros ya están a nuestro alrededor y en forma de imágenes falsas, generadas por Generative Adversarial Networks (GAN). En este blog, no me centraré en las imágenes producidas por GAN, sino en las técnicas más fundamentales, es decir, la creación de datos sintéticos basados en distribuciones de probabilidad.
Los datos sintéticos se pueden crear utilizando técnicas de muestreo en dos amplias categorías:
Muestreo probabilístico; cree datos sintéticos que reflejen fielmente la distribución de los datos reales, haciéndolos útiles para entrenar modelos de aprendizaje automático y realizar análisis estadísticos.
Muestreo no probabilístico; implica la selección de muestras sin una probabilidad de selección conocida, como el muestreo por conveniencia, el muestreo de bola de nieve y el muestreo por cuotas. Es una forma rápida, fácil y económica de obtener datos.
Me centraré en el muestreo probabilístico en el que la estimación de los parámetros de distribución de la población es clave. O, en otras palabras, buscamos la distribución teórica que mejor se ajuste en el caso de conjuntos de datos univariados. Con la distribución teórica estimada, podemos generar nuevas muestras; nuestro conjunto de datos sintéticos.
Encontrar la distribución teórica que mejor se ajuste que imite los eventos del mundo real puede ser un desafío, ya que hay muchas distribuciones de probabilidad diferentes. Las bibliotecas como distfit son muy útiles en estos casos.
En la Figura 1 se muestra una excelente descripción general de las funciones de densidad de probabilidad (PDF) donde se capturan las formas "canónicas" de las distribuciones. Tal descripción general puede ayudar a comprender mejor y decidir qué distribución puede ser la más apropiada para un caso de uso específico. En las siguientes dos secciones, experimentaremos con diferentes distribuciones y sus parámetros y veremos qué tan bien podemos generar datos sintéticos.
Los datos sintéticos son datos artificiales generados mediante modelos estadísticos.
El uso de datos sintéticos es ideal para generar conjuntos de datos grandes y diversos para la simulación y, como tal, permite probar y explorar diferentes escenarios. Esto puede ayudar a obtener percepciones y conocimientos que pueden ser difíciles o imposibles de obtener por otros medios, o donde necesitamos determinar los casos límite para sistemas y procesos. Sin embargo, la creación de datos sintéticos puede ser un desafío porque requiere imitar eventos del mundo real mediante el uso de distribución teórica y parámetros de población.
Con datos sintéticos, nuestro objetivo es imitar eventos del mundo real mediante la estimación de distribuciones teóricas y parámetros de población.
Con datos sintéticos, nuestro objetivo es imitar eventos del mundo real mediante la estimación de distribuciones teóricas y parámetros de población.
Para demostrar la creación de datos sintéticos, creé un caso de uso hipotético en el que trabajamos en el dominio de la seguridad y necesitamos comprender el comportamiento de las actividades de la red. Un experto en seguridad nos proporcionó la siguiente información; la mayoría de las actividades de la red comienzan a las 8 y alcanzan su punto máximo alrededor de las 10. Algunas actividades se verán antes de las 8, pero no muchas. Por la tarde, las actividades disminuyen gradualmente y se detienen alrededor de las 6 pm. Sin embargo, también hay un pequeño pico a las 1-2 pm. Tenga en cuenta que, en general, es mucho más difícil describir eventos anormales que lo que es un comportamiento normal/esperado debido al hecho de que el comportamiento normal se ve con mayor frecuencia y, por lo tanto, la mayor proporción de las observaciones. Traduzcamos esta información a un modelo estadístico.
Con la descripción, necesitamos decidir la mejor distribución teórica coincidente. Sin embargo, elegir la mejor distribución teórica requiere investigar las propiedades de muchas distribuciones (ver Figura 1). Además, es posible que necesite más de una distribución; es decir, una mezcla de funciones de densidad de probabilidad. En nuestro ejemplo, crearemos una combinación de dos distribuciones, un PDF para las actividades de la mañana y otro PDF para las actividades de la tarde.
Descripción mañana: "la mayoría de las actividades de la red comienzan a las 8 y alcanzan su punto máximo alrededor de las 10. Algunas actividades se verán antes de las 8, pero no muchas".
Para modelar las actividades de la red de la mañana, podemos usar la distribución Normal. Es simétrico y no tiene colas pesadas. Podemos establecer los siguientes parámetros; una media de 10 am y una dispersión relativamente estrecha, como sigma=0.5. En la Figura 2 se muestran algunas PDF normales con diferentes parámetros mu y sigma. Trate de sentir cómo cambia la pendiente en el parámetro sigma.
Descripción de la tarde: “Las actividades disminuyen gradualmente y se detienen alrededor de las 6 de la tarde. Sin embargo, también hay un pequeño pico entre la 1 y las 2 de la tarde”.
Una distribución adecuada para las actividades de la tarde podría ser una distribución sesgada con una cola derecha pesada que pueda capturar las actividades decrecientes graduales. La distribución de Weibull puede ser una candidata, ya que se utiliza para modelar datos que tienen una tendencia monotónica creciente o decreciente. Sin embargo, si no siempre esperamos una disminución monótona en la actividad de la red (porque es diferente los martes más o menos), puede ser mejor considerar una distribución como gamma (Figura 3). Aquí también debemos ajustar los parámetros para que coincida mejor con la descripción. Para tener más control sobre la forma de la distribución, de preferencia uso la distribución gamma generalizada.
En la siguiente sección, experimentaremos con las dos distribuciones candidatas (Normal y Gamma generalizada) y estableceremos los parámetros para crear una combinación de PDF que sea representativa del caso de uso de actividades de red.
En la sección de códigos de abajo, generaremos 10.000 muestras a partir de una distribución normal con una media de 10 (que representa el pico a las 10 a. m.) y una desviación estándar de 0,5. A continuación, generamos 2000 muestras a partir de una distribución gamma generalizada para la que configuro el segundo pico en loc=13. También podríamos haber elegido loc=14, pero eso resultó en una brecha más grande entre las dos distribuciones. El siguiente paso es combinar los dos conjuntos de datos y mezclarlos. Tenga en cuenta que no se requiere barajar, pero sin él, las muestras se ordenan primero por las 10.000 muestras de la distribución normal y luego por las 1000 muestras de la distribución gamma generalizada. Este orden podría introducir sesgos en cualquier análisis o modelado que se realice en el conjunto de datos al dividir el conjunto de datos.
import numpy as np
import matplotlib.pyplot as plt
from distfit import distfit
from scipy.stats import norm, gengamma
np.random.seed(1)
# Generar datos a partir de una distribución normal
normal_samples = norm.rvs(10, 1, 10000)
# Cree una distribución gamma generalizada con los parámetros especificados
dist = gengamma(a=1.4, c=1, scale=0.8, loc=13)
# Generar muestras aleatorias a partir de la distribución.
gamma_samples = dist.rvs(size=2000)
# Combine los dos conjuntos de datos por concatenación
dataset = np.concatenate((normal_samples, gamma_samples))
# Mezclar el conjunto de datos
np.random.shuffle(dataset)
# Gráfico
bar_properties={'color': '#607B8B', 'linewidth': 1, 'edgecolor': '#5A5A5A'}
plt.figure(figsize=(20, 15)); plt.hist(dataset, bins=100, **bar_properties)
plt.grid(True)
plt.xlabel('Time', fontsize=22)
plt.ylabel('Frequency', fontsize=22)
# Tracemos la distribución y veamos cómo se ve (Figura 3).
# Por lo general, se necesitan algunas iteraciones para
# modificar los parámetros y realizar ajustes.
Text(0, 0.5, 'Frequency')
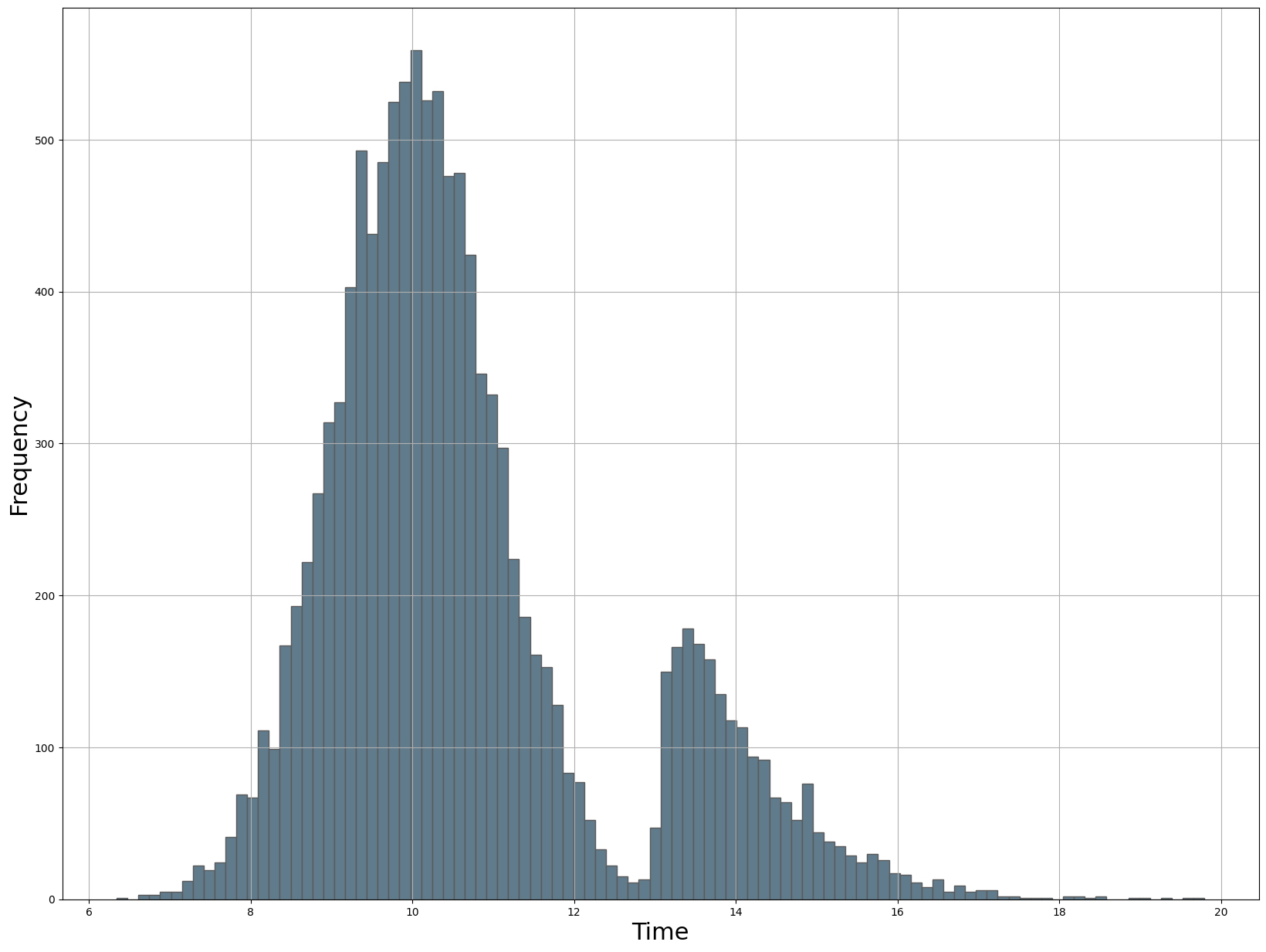
Creamos datos sintéticos utilizando una combinación de dos distribuciones para modelar el comportamiento normal/esperado de la actividad de la red para una población específica (Figura 4). Modelamos un pico importante a las 10 am con actividades de red desde las 6 am hasta la 1 pm. Se modela un segundo pico alrededor de la 1-2 p. m. con una cola derecha pesada hacia las 8 p. m. El siguiente paso podría ser establecer los intervalos de confianza y buscar la detección de valores atípicos. Puede encontrar más detalles sobre la detección de valores atípicos en el siguiente blog:
Hasta este punto, creamos datos sintéticos que permiten explorar diferentes escenarios por simulación. Aquí, crearemos datos sintéticos que reflejen fielmente la distribución de datos reales. Para la demostración, usaré el conjunto de datos de consejos de dinero de Seaborn [4] y estimaré los parámetros usando la biblioteca distfit. Recomiendo leer el blog sobre distfit si es nuevo en la estimación de funciones de densidad de probabilidad. El conjunto de datos de consejos contiene solo 244 puntos de datos. Primero inicialicemos la biblioteca, carguemos el conjunto de datos y tracemos los valores (consulte la sección de código a continuación).
# Inicializar distfit
dfit = distfit(distr='popular')
# Importar conjunto de datos
df = dfit.import_example(data='tips')
print(df.head())
# Hacer Gráfico
dfit.lineplot(df['tip'], xlabel='Número', ylabel='Valor de la propina')
[distfit] >INFO> Downloading and processing [tips] from github source. No artists with labels found to put in legend. Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
total_bill tip sex smoker day time size 0 16.99 1.01 Female No Sun Dinner 2 1 10.34 1.66 Male No Sun Dinner 3 2 21.01 3.50 Male No Sun Dinner 3 3 23.68 3.31 Male No Sun Dinner 2 4 24.59 3.61 Female No Sun Dinner 4
(<Figure size 2500x1200 with 1 Axes>, <AxesSubplot:xlabel='Número', ylabel='Valor de la propina'>)
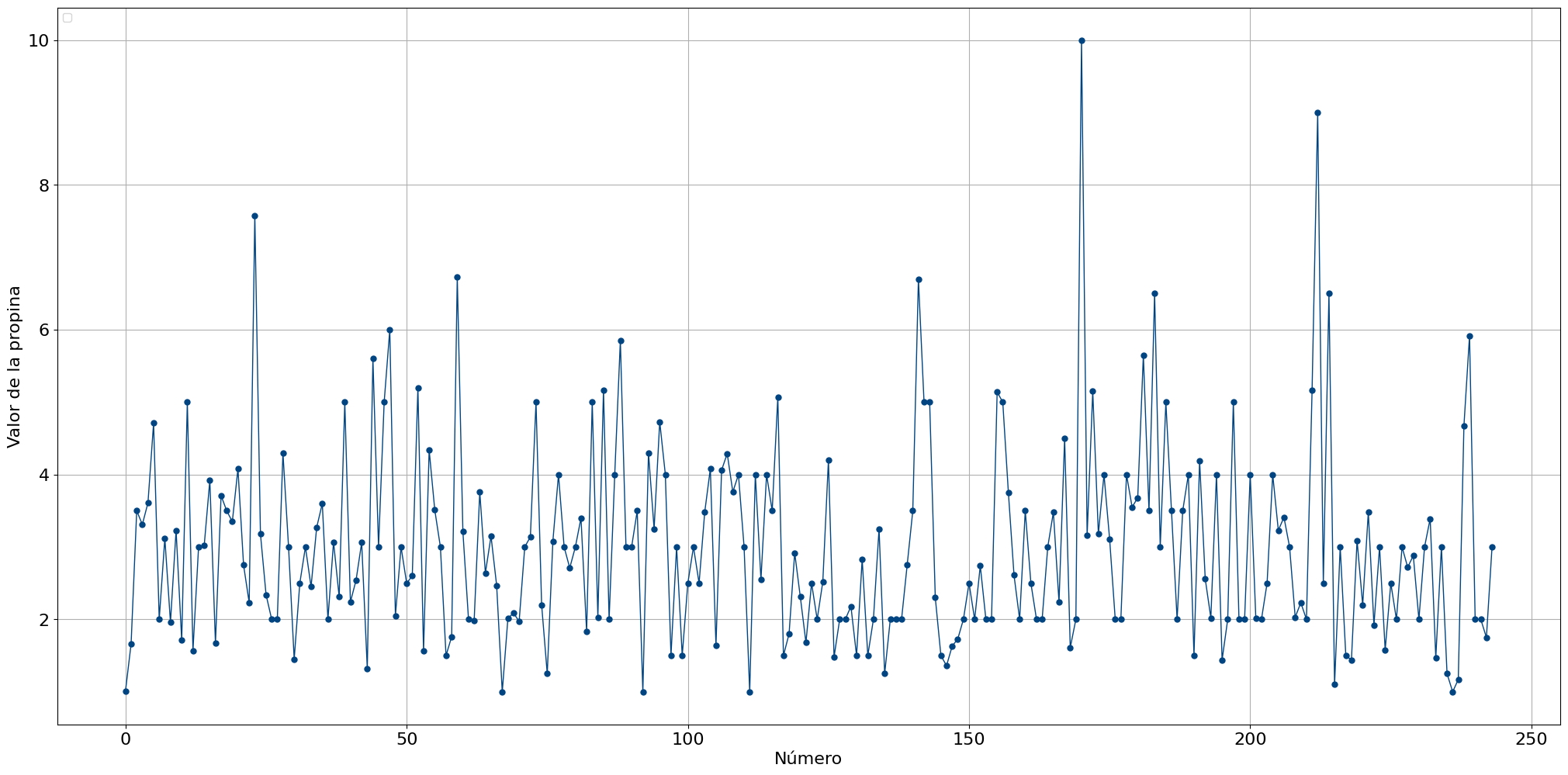
Después de cargar los datos, podemos hacer una inspección visual para tener una idea del rango y posibles valores atípicos (Figura 5). El rango entre las 244 puntas es principalmente entre 2 y 4 dólares. Con base en esta gráfica, también podemos construir una intuición de la distribución esperada cuando proyectamos todos los puntos de datos hacia el eje y (lo demostraré más adelante).
El espacio de búsqueda de distfit se establece en los PDF populares, y el parámetro de suavizado se establece en 3. Los tamaños de muestra bajos pueden hacer que el histograma tenga baches y causar ajustes de distribución deficientes.
# Inicializar con suavizado e intervalo de confianza de límite superior
dfit = distfit(smooth=3, bound='up')
# Modelo de ajuste
dfit.fit_transform(df['tip'], n_boots=100)
# Graficar PDF/CDF
fig, ax = plt.subplots(1,2, figsize=(25, 10))
dfit.plot(chart='PDF', n_top=10, ax=ax[0])
dfit.plot(chart='CDF', n_top=10, ax=ax[1])
plt.show()
# Crear gráfico de línea
dfit.lineplot(df['tip'], xlabel='Número', ylabel='Valor de la propina', projection=True)
[distfit] >INFO> fit [distfit] >INFO> transform [distfit] >INFO> [smoothline] >Smoothing by interpolation.. [distfit] >INFO> [norm ] [0.51 sec] [RSS: 0.0156694] [loc=2.998 scale=1.381] [distfit] >INFO> [expon ] [0.46 sec] [RSS: 0.146759] [loc=1.000 scale=1.998] [distfit] >INFO> [pareto ] [8.17 sec] [RSS: 0.275503] [loc=-0.211 scale=1.211] [distfit] >INFO> [dweibull ] [5.08 sec] [RSS: 0.0169087] [loc=2.801 scale=1.112] [distfit] >INFO> [t ] [13.4 sec] [RSS: 0.0103655] [loc=2.812 scale=1.060] [distfit] >INFO> [genextreme] [13.4 sec] [RSS: 0.0153201] [loc=2.344 scale=0.957] [distfit] >INFO> [gamma ] [6.01 sec] [RSS: 0.0135448] [loc=0.813 scale=0.852] [distfit] >INFO> [lognorm ] [11.3 sec] [RSS: 0.0150311] [loc=0.218 scale=2.483] [distfit] >INFO> [beta ] [13.2 sec] [RSS: 0.00757804] [loc=-0.173 scale=13.910] [distfit] >INFO> [uniform ] [0.38 sec] [RSS: 0.223683] [loc=1.000 scale=9.000] [distfit] >INFO> [loggamma ] [15.6 sec] [RSS: 0.0175704] [loc=-505.876 scale=66.339] [distfit] >INFO> Compute confidence intervals [parametric] [distfit] >INFO> Create PDF plot for the parametric method. [distfit] >INFO> Estimated distribution: Beta(loc:-0.173207, scale:13.909676) [distfit] >INFO> Create CDF plot for the parametric method. [distfit] >INFO> Ploting CDF
[distfit] >INFO> [smoothline] >Smoothing by interpolation..
(<Figure size 2500x1200 with 1 Axes>,
<AxesSubplot:title={'center':'\nbeta(a=3.83986, b=12.9412, loc=-0.173207, scale=13.9097)'},
xlabel='Número', ylabel='Valor de la propina'>)
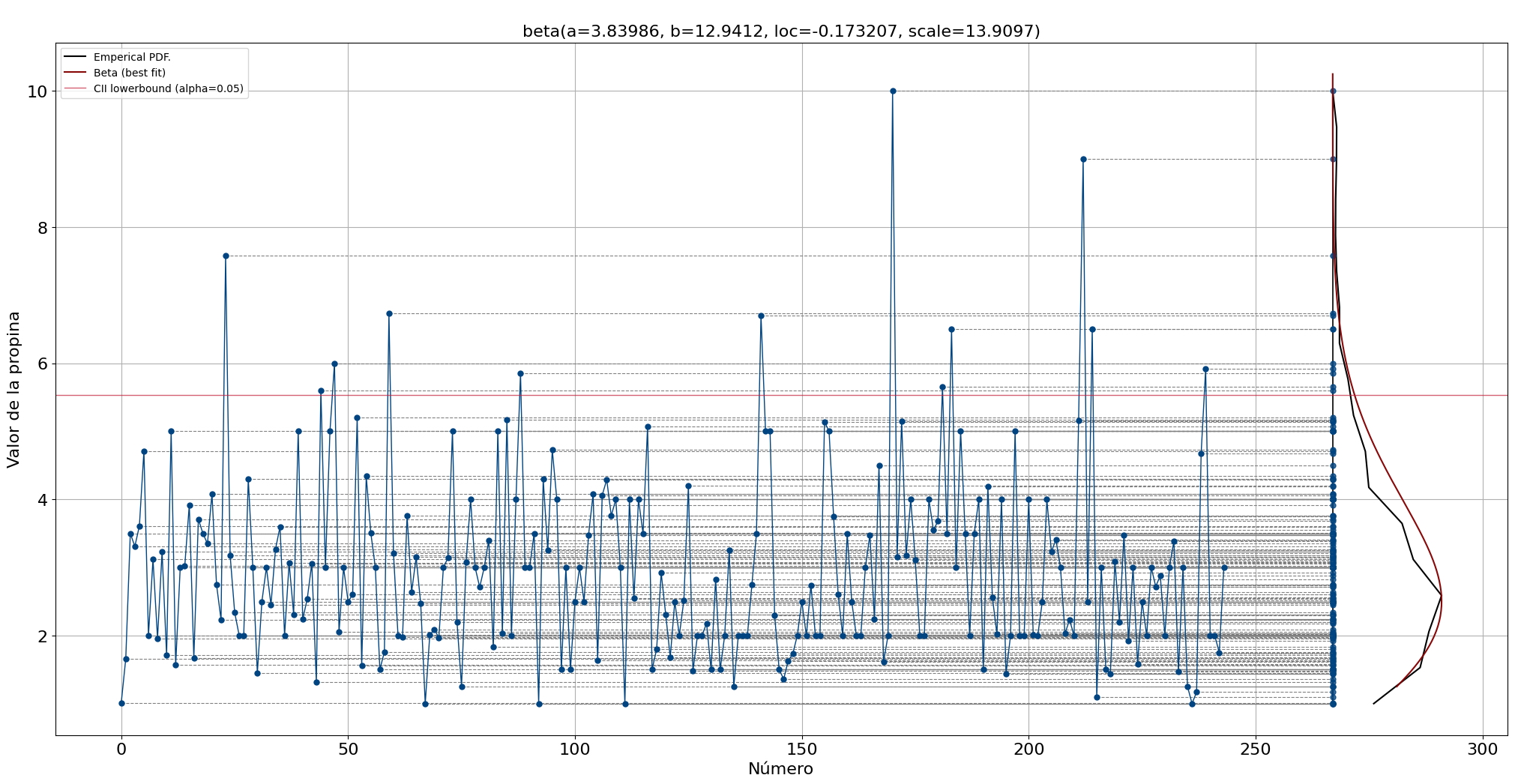
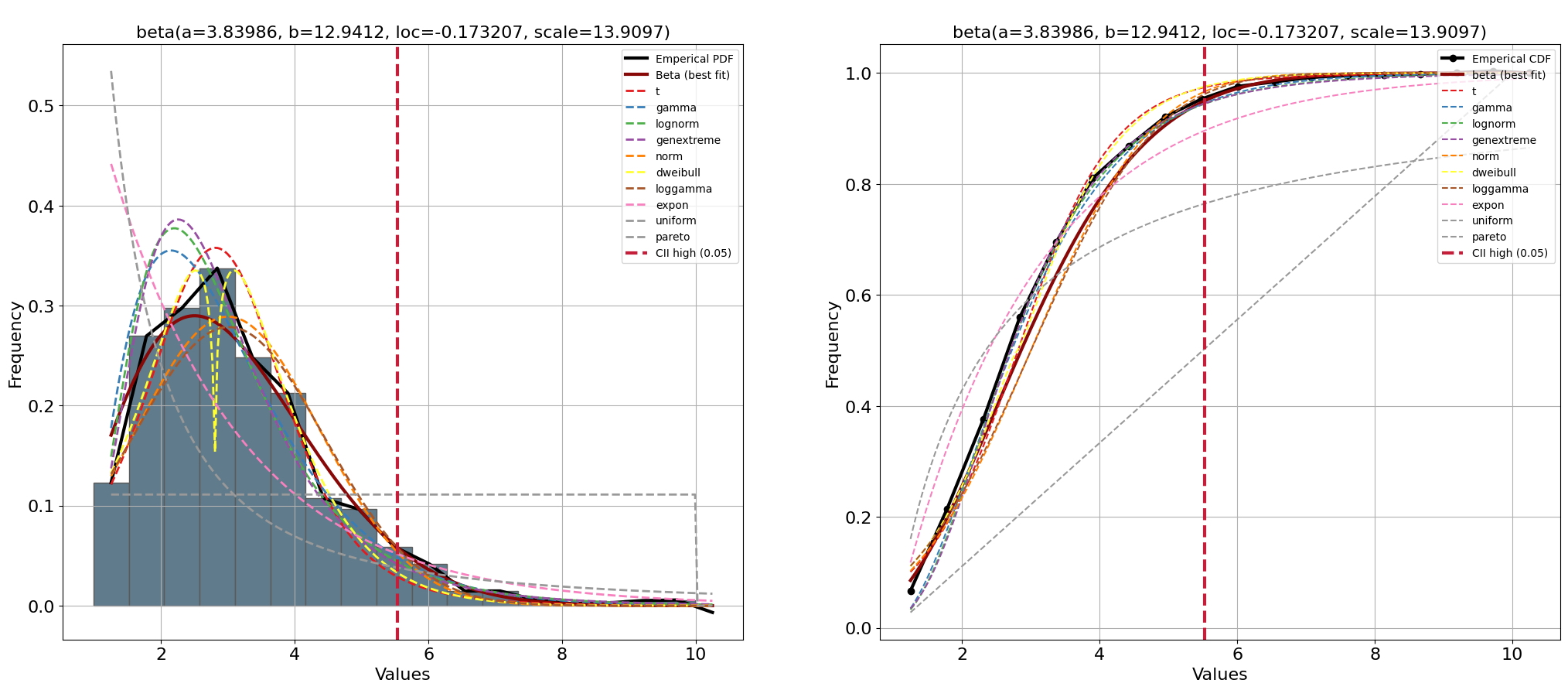
El PDF que mejor se ajusta es beta. El límite superior del intervalo de confianza alfa = 0,05 es 5,53, que parece un umbral razonable basado en una inspección visual (línea vertical roja).
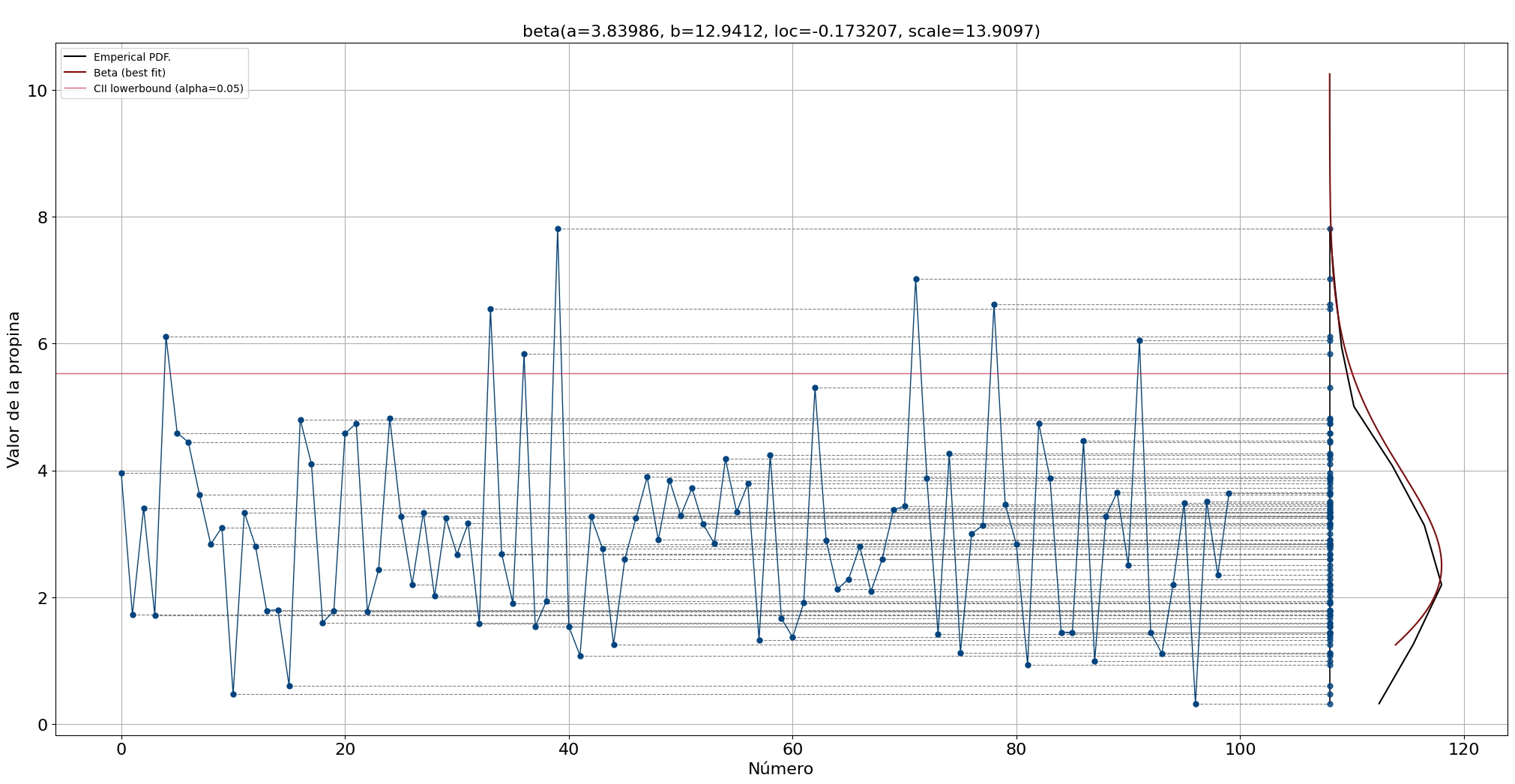
Después de encontrar la mejor distribución, podemos proyectar el PDF estimado en la parte superior de nuestro gráfico de líneas para una mejor intuición. Tenga en cuenta que tanto el PDF como el PDF empírico son exactamente iguales a los de la figura.
Con los parámetros estimados para la distribución que mejor se ajuste, podemos comenzar a crear datos sintéticos para propinas monetarias (consulte la sección de código a continuación). Creemos 100 muestras nuevas y tracemos los puntos de datos. Los datos sintéticos brindan muchas oportunidades, es decir, se pueden usar para entrenar modelos, pero también para obtener información sobre cuestiones como el tiempo que llevaría ahorrar una cierta cantidad de dinero usando propinas.
# Crear datos sintéticos
X = dfit.generate(100)
# Graficar los datos
dfit.lineplot(X, xlabel='Número', ylabel='Valor de la propina', grid=True)
[distfit] >INFO> Create Synthetic data for 100 beta distributed samples with fitted params (3.8398602263040145, 12.941240498249325, -0.17320742358898006, 13.909676436498582). [distfit] >INFO> [smoothline] >Smoothing by interpolation..
(<Figure size 2500x1200 with 1 Axes>,
<AxesSubplot:title={'center':'\nbeta(a=3.83986, b=12.9412, loc=-0.173207, scale=13.9097)'},
xlabel='Número', ylabel='Valor de la propina'>)