Volver al Inicio

Anterior Siguiente

15 de Mayo del 2022 | Jhonatan Montilla

Detección de Valores Atípicos utilizando Análisis de Componentes Principales (PCA)

Gracias a la sensibilidad de PCA, se puede utilizar para detectar valores atípicos en conjuntos de datos multivariados. También haremos uso de los métodos T2 y SPE/DmodX de Hotelling.

El Análisis de Componentes Principales (PCA) es una técnica ampliamente utilizada para la reducción de la dimensionalidad mientras se preserva la información relevante. Debido a su sensibilidad, también se puede utilizar para detectar valores atípicos en conjuntos de datos multivariados. La detección de valores atípicos puede proporcionar señales de alerta temprana para condiciones anormales, lo que permite a los expertos identificar y abordar los problemas antes de que se intensifiquen. Sin embargo, la detección de valores atípicos en conjuntos de datos multivariados puede ser un desafío debido a la alta dimensionalidad y la falta de etiquetas. PCA ofrece varias ventajas para la detección de valores atípicos. Describiré los conceptos de detección de valores atípicos mediante PCA. Con un ejemplo práctico, demostraré cómo crear un modelo no supervisado para la detección de valores atípicos para conjuntos de datos categóricos continuos y por separado.

Detección de valores atípicos.

Los valores atípicos se pueden modelar en un enfoque univariante o multivariante (Figura 1). En el enfoque univariante, los valores atípicos se detectan utilizando una variable a la vez, para lo cual el análisis de distribución de datos es una excelente manera. Lea más detalles sobre la detección de valores atípicos univariados en la siguiente publicación de blog:

El enfoque multivariado utiliza múltiples características y, por lo tanto, puede detectar valores atípicos con relaciones (no) lineales o distribuciones sesgadas. La biblioteca scikit-learn tiene varias soluciones para la detección de valores atípicos multivariados, como el clasificador de una clase, el bosque de aislamiento y el factor local de valores atípicos. En este blog, me centraré en la detección de valores atípicos multivariados mediante el análisis de componentes principales, que tiene sus propias ventajas, como la explicabilidad; los valores atípicos se pueden visualizar ya que confiamos en la reducción de dimensionalidad de PCA en sí.

Anomalías vs. Novedades.

Las anomalías y novedades son observaciones desviadas del comportamiento estándar/esperado. También denominados valores atípicos. Sin embargo, existen algunas diferencias: las anomalías son desviaciones que se han visto antes, generalmente utilizadas para detectar fraude, intrusión o mal funcionamiento. Las novedades son desviaciones que no se han visto antes o que se utilizan para identificar nuevos patrones o eventos. En tales casos, es importante utilizar el conocimiento del dominio. Tanto las anomalías como las novedades pueden ser difíciles de detectar, ya que la definición de lo que es normal o esperado puede ser subjetiva y variar según la aplicación.

Análisis de componentes principales para la detección de valores atípicos.

El análisis de componentes principales (PCA) es una transformación lineal que reduce la dimensionalidad y busca la dirección en los datos con la mayor variación. Debido a la naturaleza del método, es sensible a variables con diferentes rangos de valores y, por lo tanto, también a valores atípicos. Una ventaja es que permite la visualización de los datos en un diagrama de dispersión de dos o tres dimensiones, lo que facilita la confirmación visual de los valores atípicos detectados. Además, proporciona una buena interpretabilidad de las variables de respuesta. Otra gran ventaja de PCA es que se puede combinar con otros métodos, como diferentes métricas de distancia, para mejorar la precisión de la detección de valores atípicos. Aquí usaré la biblioteca PCA que contiene dos métodos para la detección de valores atípicos: T2 de Hotelling y SPE/DmodX. Para obtener más detalles, lea la publicación de blog sobre el análisis de componentes principales y la biblioteca pca.

Detección de valores atípicos para variables aleatorias continuas.

Comencemos con un ejemplo para demostrar el funcionamiento de la detección de valores atípicos utilizando T2 de Hotelling y SPE/DmodX para variables aleatorias continuas. Usaré el conjunto de datos de vino de sklearn que contiene 178 muestras, con 13 características y 3 clases de vino.

from sklearn.datasets import load_wine
import pandas as pd
import numpy as np
from pca import pca
from df2onehot import df2onehot

data = load_wine()
df = pd.DataFrame(index=data.target, data=data.data, columns=data.feature_names)
df.head()

	alcohol	malic_acid	ash	alcalinity_of_ash	magnesium	total_phenols	flavanoids	nonflavanoid_phenols	proanthocyanins	color_intensity	hue	od280/od315_of_diluted_wines	proline
0	14.23	1.71	2.43	15.6	127.0	2.80	3.06	0.28	2.29	5.64	1.04	3.92	1065.0
0	13.20	1.78	2.14	11.2	100.0	2.65	2.76	0.26	1.28	4.38	1.05	3.40	1050.0
0	13.16	2.36	2.67	18.6	101.0	2.80	3.24	0.30	2.81	5.68	1.03	3.17	1185.0
0	14.37	1.95	2.50	16.8	113.0	3.85	3.49	0.24	2.18	7.80	0.86	3.45	1480.0
0	13.24	2.59	2.87	21.0	118.0	2.80	2.69	0.39	1.82	4.32	1.04	2.93	735.0

model = pca(normalize=True, detect_outliers=['ht2', 'spe'], n_std=2)
results = model.fit_transform(df)
results['outliers']

[pca] >Processing dataframe..
[pca] >Normalizing input data per feature (zero mean and unit variance)..
[pca] >The PCA reduction is performed to capture [95.0%] explained variance using the
[13] columns of the input data.
[pca] >Fit using PCA.
[pca] >Compute loadings and PCs.
[pca] >Compute explained variance.
[pca] >Number of components is [10] that covers the [95.00%] explained variance.
[pca] >The PCA reduction is performed on the [13] columns of the input dataframe.
[pca] >Fit using PCA.
[pca] >Compute loadings and PCs.
[pca] >Outlier detection using Hotelling T2 test with alpha=[0.05] and n_components=[10]
[pca] >Multiple test correction applied for Hotelling T2 test: [fdr_bh]
[pca] >Outlier detection using SPE/DmodX with n_std=[2]

	y_proba	p_raw	y_score	y_bool	y_bool_spe	y_score_spe
0	0.982875	0.376726	21.351215	False	False	3.617239
0	0.982875	0.624371	17.438087	False	False	2.234477
0	0.982875	0.589438	17.969195	False	False	2.719789
0	0.982875	0.134454	27.028857	False	True	4.659735
0	0.982875	0.883264	12.861094	False	False	1.332104
...	...	...	...	...	...	...
2	0.982875	0.147396	26.583414	False	True	4.033903
2	0.982875	0.771408	15.087004	False	False	3.139750
2	0.982875	0.244157	23.959708	False	True	3.846217
2	0.982875	0.333600	22.128104	False	False	3.312952
2	0.982875	0.138437	26.888278	False	True	4.238283

178 rows × 6 columns

Después de ejecutar la función de ajuste, la biblioteca pca calificará la muestra si una muestra es un valor atípico. Para cada muestra, se recopilan múltiples estadísticas, como se muestra en la sección de código a continuación. Las primeras cuatro columnas en el marco de datos (y_proba, p_raw, y_score e y_bool) son valores atípicos detectados mediante el método T2 de Hotelling. Las dos últimas columnas (y_bool_spe y y_score_spe) se basan en el método SPE/DmodX.

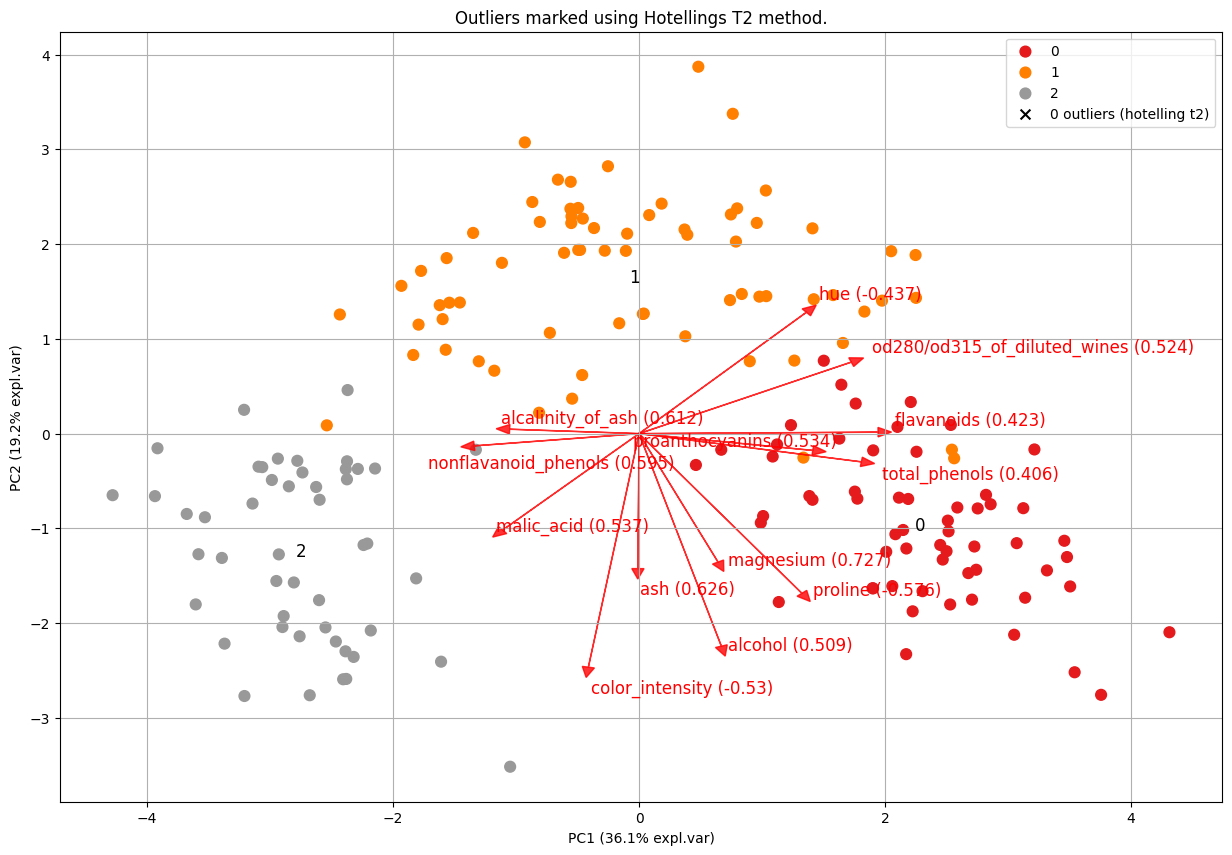
El T2 de Hotelling calcula las pruebas de chi-cuadrado y los valores P en los n_componentes principales, lo que permite clasificar los valores atípicos de fuerte a débil usando y_proba. Tenga en cuenta que el espacio de búsqueda de valores atípicos abarca las dimensiones PC1 a PC5, ya que se espera que la varianza más alta (y, por lo tanto, los valores atípicos) se observe en los primeros componentes. Tenga en cuenta que la profundidad es opcional en caso de que la varianza no se capture bien en los primeros cinco componentes. Tracemos los valores atípicos y marquémoslos para los conjuntos de datos de vino (Figura 2).

model.biplot(SPE=False, hotellingt2=True,
title='Outliers marked using Hotellings T2 method.')

[pca] >Plot PC1 vs PC2 with loadings.

(<Figure size 1500x1000 with 1 Axes>,
<AxesSubplot:title={'center':'Outliers marked using Hotellings T2 method.'},
xlabel='PC1 (36.1% expl.var)', ylabel='PC2 (19.2% expl.var)'>)

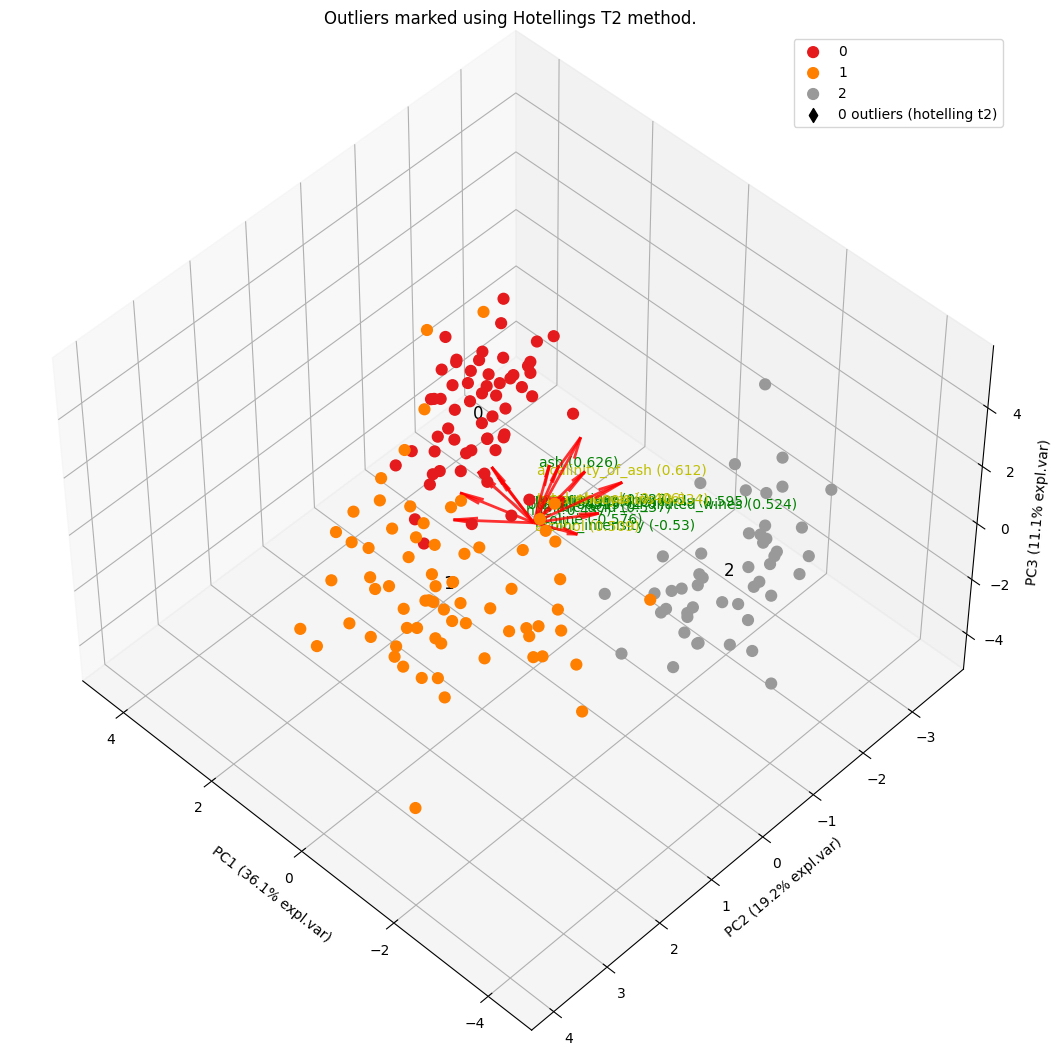
model.biplot3d(SPE=False, hotellingt2=True,
  title='Outliers marked using Hotellings T2 method.')

[pca] >Plot PC1 vs PC2 vs PC3 with loadings.

(<Figure size 1500x1000 with 2 Axes>,
<Axes3D:title={'center':'Outliers marked using Hotellings T2 method.'},
xlabel='PC1 (36.1% expl.var)', ylabel='PC2 (19.2% expl.var)'>)

df.loc[results['outliers']['y_bool'], :]

	alcohol	malic_acid	ash	alcalinity_of_ash	magnesium	total_phenols	flavanoids	nonflavanoid_phenols	proanthocyanins	color_intensity	hue	od280/od315_of_diluted_wines	proline

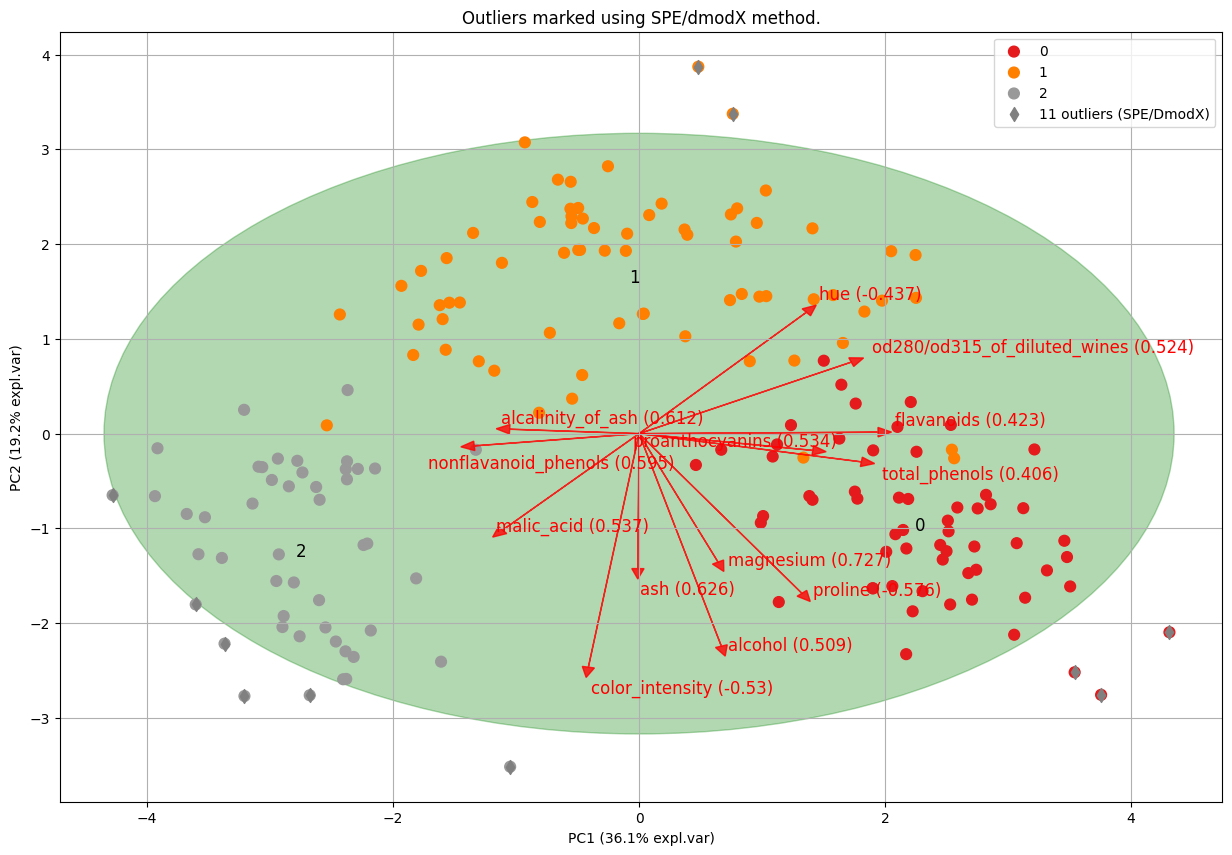
El método SPE/DmodX calcula la distancia euclidiana entre las muestras individuales y el centro. Podemos visualizar esto con una elipse verde. Una muestra se marca como un valor atípico en función de la media y la covarianza de las dos primeras PC (Figura 3). En otras palabras, cuando está fuera de la elipse.

model.biplot(SPE=True, hotellingt2=False, title='Outliers marked using SPE/dmodX method.')
  

[pca] >Plot PC1 vs PC2 with loadings.

(<Figure size 1500x1000 with 1 Axes>,
<AxesSubplot:title={'center':'Outliers marked using SPE/dmodX method.'},
xlabel='PC1 (36.1% expl.var)', ylabel='PC2 (19.2% expl.var)'>)

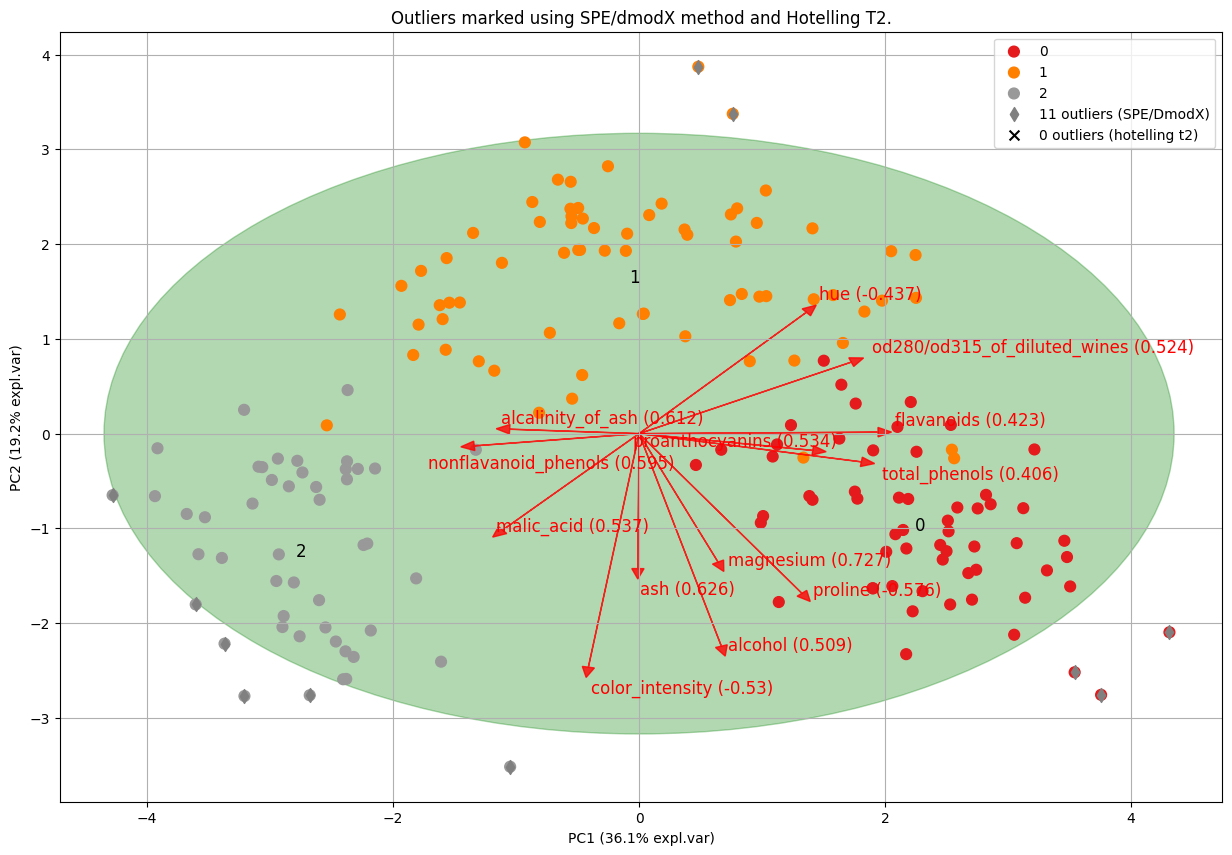
model.biplot(SPE=True, hotellingt2=True,
title='Outliers marked using SPE/dmodX method and Hotelling T2.')

[pca] >Plot PC1 vs PC2 with loadings.

(<Figure size 1500x1000 with 1 Axes>,
<AxesSubplot:title={'center':'Outliers marked using SPE/dmodX method and Hotelling T2.'}, 
xlabel='PC1 (36.1% expl.var)', ylabel='PC2 (19.2% expl.var)'>)

df.loc[results['outliers']['y_bool_spe'], :]

	alcohol	malic_acid	ash	alcalinity_of_ash	magnesium	total_phenols	flavanoids	nonflavanoid_phenols	proanthocyanins	color_intensity	hue	od280/od315_of_diluted_wines	proline
0	14.37	1.95	2.50	16.8	113.0	3.85	3.49	0.24	2.18	7.8	0.86	3.45	1480.0
0	14.38	1.87	2.38	12.0	102.0	3.30	3.64	0.29	2.96	7.5	1.20	3.00	1547.0
0	14.19	1.59	2.48	16.5	108.0	3.30	3.93	0.32	1.86	8.7	1.23	2.82	1680.0
1	12.00	0.92	2.00	19.0	86.0	2.42	2.26	0.30	1.43	2.5	1.38	3.12	278.0
1	11.03	1.51	2.20	21.5	85.0	2.46	2.17	0.52	2.01	1.9	1.71	2.87	407.0
2	13.88	5.04	2.23	20.0	80.0	0.98	0.34	0.40	0.68	4.9	0.58	1.33	415.0
2	13.17	5.19	2.32	22.0	93.0	1.74	0.63	0.61	1.55	7.9	0.60	1.48	725.0
2	14.34	1.68	2.70	25.0	98.0	2.80	1.31	0.53	2.70	13.0	0.57	1.96	660.0
2	13.71	5.65	2.45	20.5	95.0	1.68	0.61	0.52	1.06	7.7	0.64	1.74	740.0
2	13.27	4.28	2.26	20.0	120.0	1.59	0.69	0.43	1.35	10.2	0.59	1.56	835.0
2	14.13	4.10	2.74	24.5	96.0	2.05	0.76	0.56	1.35	9.2	0.61	1.60	560.0

Usando los resultados de ambos métodos, ahora también podemos calcular la superposición. En este caso de uso, hay 5 valores atípicos que se superponen (consulte la sección de código a continuación).

I_overlap = np.logical_and(results['outliers']['y_bool'], results['outliers']['y_bool_spe'])
df.loc[I_overlap, :]

	alcohol	malic_acid	ash	alcalinity_of_ash	magnesium	total_phenols	flavanoids	nonflavanoid_phenols	proanthocyanins	color_intensity	hue	od280/od315_of_diluted_wines	proline

Detección de valores atípicos para variables categóricas.

Para la detección de valores atípicos en variables categóricas, primero debemos discretizar las variables categóricas y hacer que las distancias sean comparables entre sí. Con el conjunto de datos discretizados (one-hot), podemos proceder usando el enfoque PCA y aplicar los métodos T2 y SPE/DmodX de Hotelling. Usaré el conjunto de datos Student Performance [5] para fines de demostración, que contiene 649 muestras y 33 variables. Importaremos el conjunto de datos como se muestra en la sección de código a continuación. Puede encontrar más detalles sobre la descripción de la columna aquí. No eliminaré ninguna columna, pero si hubiera una columna de identificador o variables con tipo flotante, las habría eliminado o categorizado en contenedores discretos.

model = pca()
df = model.import_example(data='student')
df.head()

[pca] >Downloading example dataset from github source..
[pca] >Import dataset [student]

	school	sex	age	address	famsize	Pstatus	Medu	Fedu	Mjob	Fjob	...	famrel	freetime	goout	Dalc	Walc	health	absences	G1	G2	G3
0	GP	F	18	U	GT3	A	4	4	at_home	teacher	...	4	3	4	1	1	3	4	0	11	11
1	GP	F	17	U	GT3	T	1	1	at_home	other	...	5	3	3	1	1	3	2	9	11	11
2	GP	F	15	U	LE3	T	1	1	at_home	other	...	4	3	2	2	3	3	6	12	13	12
3	GP	F	15	U	GT3	T	4	2	health	services	...	3	2	2	1	1	5	0	14	14	14
4	GP	F	16	U	GT3	T	3	3	other	other	...	4	3	2	1	2	5	0	11	13	13

5 rows × 33 columns

Las variables deben codificarse en caliente para asegurarse de que las distancias entre las variables sean comparables entre sí. Esto da como resultado 177 columnas para 649 muestras (consulte la sección de código a continuación).

df_hot = df2onehot(df)['onehot']
df_hot.head()

[df2onehot] >Auto detecting dtypes.

100%|██████████| 33/33 [00:00<00:00, 47.40it/s]

[df2onehot] >Set dtypes in dataframe..

100%|██████████| 33/33 [00:00<00:00, 47.64it/s]

[df2onehot] >Total onehot features: 177

	school_GP	school_MS	sex_F	sex_M	age_15.0	age_16.0	age_17.0	age_18.0	age_19.0	age_20.0	...	G3_15.0	G3_16.0	G3_17.0	G3_18.0	G3_19.0	G3_5.0	G3_6.0	G3_7.0	G3_8.0	G3_9.0
0	True	False	True	False	False	False	False	True	False	False	...	False	False	False	False	False	False	False	False	False	False
1	True	False	True	False	False	False	True	False	False	False	...	False	False	False	False	False	False	False	False	False	False
2	True	False	True	False	True	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	False
3	True	False	True	False	True	False	False	False	False	False	...	False	False	False	False	False	False	False	False	False	False
4	True	False	True	False	False	True	False	False	False	False	...	False	False	False	False	False	False	False	False	False	False

5 rows × 177 columns

Ahora podemos usar el marco de datos one-hot procesado como entrada para pca y detectar valores atípicos. Durante la inicialización, podemos configurar normalize=True para normalizar los datos y necesitamos especificar los métodos de detección de valores atípicos.

model = pca(normalize=True,
            detect_outliers=['ht2', 'spe'],
            alpha=0.05,
            n_std=3,
            multipletests='fdr_bh')
results = model.fit_transform(df_hot)
overlapping_outliers = np.logical_and(results['outliers']['y_bool'],
                                      results['outliers']['y_bool_spe'])
df.loc[overlapping_outliers]

[pca] >Processing dataframe..
[pca] >Normalizing input data per feature (zero mean and unit variance)..
[pca] >The PCA reduction is performed to capture [95.0%] explained variance using the
[177] columns of the input data.
[pca] >Fit using PCA.
[pca] >Compute loadings and PCs.
[pca] >Compute explained variance.
[pca] >Number of components is [116] that covers the [95.00%] explained variance.
[pca] >The PCA reduction is performed on the [177] columns of the input dataframe.
[pca] >Fit using PCA.
[pca] >Compute loadings and PCs.
[pca] >Outlier detection using Hotelling T2 test with alpha=[0.05] and n_components=[116]
[pca] >Multiple test correction applied for Hotelling T2 test: [fdr_bh]
[pca] >Outlier detection using SPE/DmodX with n_std=[3]

	school	sex	age	address	famsize	Pstatus	Medu	Fedu	Mjob	Fjob	...	famrel	freetime	goout	Dalc	Walc	health	absences	G1	G2	G3
279	GP	M	22	U	GT3	T	3	1	services	services	...	5	4	5	5	5	1	12	7	8	5
284	GP	M	18	U	GT3	T	2	1	services	services	...	3	2	5	2	5	5	4	7	8	6
523	MS	M	18	U	LE3	T	4	4	at_home	health	...	5	5	5	5	5	5	2	5	6	6
605	MS	F	19	U	GT3	T	1	1	at_home	services	...	5	5	5	2	3	2	0	5	0	0
610	MS	F	19	R	GT3	A	1	1	at_home	at_home	...	3	5	4	1	4	1	0	8	0	0

5 rows × 33 columns

La prueba Hotelling T2 detectó 85 valores atípicos y el método SPE/DmodX detectó 6 valores atípicos (Figura 4, ver leyenda). El número de valores atípicos que se superponen entre ambos métodos es 5. Podemos hacer un gráfico con la funcionalidad biplot y colorear las muestras en cualquier categoría para una mayor investigación (como la etiqueta de sexo). Los valores atípicos están marcados con x o *. Este es ahora un buen comienzo para una inspección más profunda; en nuestro caso, podemos ver en la Figura 4 que los 5 valores atípicos se están alejando de todas las demás muestras. Podemos clasificar los valores atípicos, observar las cargas e investigar más profundamente a estos estudiantes (consulte la sección de código anterior). Para clasificar los valores atípicos, podemos usar y_proba (cuanto más bajo, mejor) para el método Hotelling T2, y y_score_spe, para el método SPE/DmodX. Esta última es la distancia euclidiana de la muestra al centro (por lo tanto, cuanto más grande, mejor).

model.biplot(SPE=True,
             hotellingt2=True,
             jitter=0.1,
             n_feat=10,
             legend=True,
             label=False,
             y=df['sex'],
             title='Student Performance',
             figsize=(20, 12),
             color_arrow='k',
             fontdict={'size':16, 'c':'k'},
             cmap='bwr_r',
             gradient='#FFFFFF',
             )

[pca] >Plot PC1 vs PC2 with loadings.

(<Figure size 2000x1200 with 1 Axes>,
<AxesSubplot:title={'center':'Student Performance'}, xlabel='PC1 (3.94% expl.var)', 
ylabel='PC2 (2.47% expl.var)'>)

Comentarios.

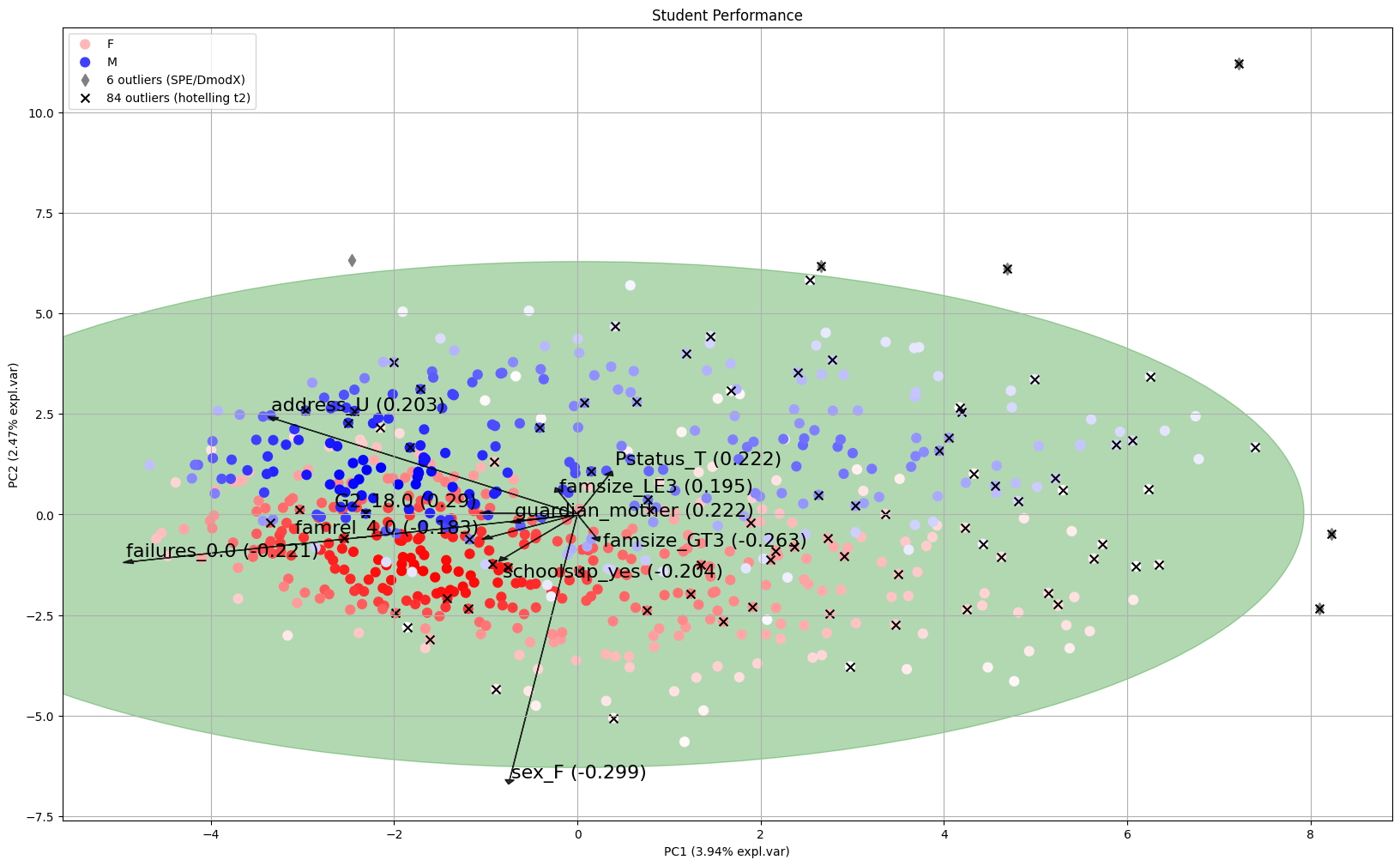
Hemos demostrado cómo usar PCA para la detección de valores atípicos multivariados para variables continuas y categóricas. Con la biblioteca PCA, podemos usar el método T2 de Hotelling y/o el método SPE/DmodX para determinar los valores atípicos candidatos. La interpretación de la contribución de cada variable a los componentes principales se puede recuperar utilizando las cargas y visualizarse con el biplot en el espacio de PC de baja dimensión. Tales conocimientos visuales pueden ayudar a proporcionar intuición sobre los valores atípicos de detección y si requieren un análisis de seguimiento. En general, la detección de valores atípicos puede ser un desafío porque determinar qué se considera normal puede ser subjetivo y variar según la aplicación específica.