 Volver al Inicio
Volver al Inicio
 Volver al Inicio
Volver al Inicio
10 de Julio del 2022 | Jhonatan Montilla
La detección de anomalías o novedades es aplicable en una amplia gama de situaciones en las que se requiere una advertencia clara y temprana de una condición anormal, como datos de sensores, operaciones de seguridad y detección de fraude, entre otros. Debido a la naturaleza del problema, los valores atípicos no se presentan con frecuencia y, debido a la falta de etiquetas, puede resultar difícil crear modelos supervisados. Los valores atípicos también se denominan anomalías o novedades, pero existen algunas diferencias fundamentales en los supuestos subyacentes y el proceso de modelado. Aquí discutiré las diferencias fundamentales entre anomalías y novedades y los conceptos de detección de valores atípicos. Con un ejemplo práctico, demostraré cómo crear un modelo no supervisado para la detección de anomalías y novedades mediante el ajuste de densidad de probabilidad para conjuntos de datos univariados. La biblioteca distfit se usa en todos los ejemplos.
Tanto las anomalías como las novedades son observaciones que se desvían de lo que es estándar, normal o esperado. El nombre colectivo para tales observaciones es el valor atípico. En general, los valores atípicos se presentan en la cola (relativa) de una distribución y están lejos del resto de la densidad. Además, si observa grandes picos en la densidad para un valor dado o un pequeño rango de valores, puede apuntar hacia posibles valores atípicos. Aunque el objetivo de la detección de anomalías y novedades es el mismo, existen algunas diferencias de modelado conceptual [1], que se resumen brevemente a continuación:
Las anomalías son valores atípicos que se sabe que están presentes en los datos de entrenamiento y se desvían de lo normal o esperado. En tales casos, deberíamos tratar de ajustar un modelo a las observaciones que tienen el comportamiento normal/esperado (también llamados valores internos) e ignorar las observaciones desviadas. Las observaciones que quedan fuera del comportamiento normal/esperado son los valores atípicos.
Las novedades son valores atípicos que no se sabe que estén presentes en los datos de entrenamiento. Los datos no contienen observaciones que se desvíen de lo normal/esperado. La detección de novedad puede ser más desafiante ya que no hay referencia de un valor atípico. El conocimiento del dominio es más importante en tales casos para evitar el sobreajuste del modelo en los valores internos.
Acabo de señalar que la diferencia entre anomalías y novedades está en el proceso de modelado. Pero hay más. Antes de que podamos comenzar a modelar, debemos establecer algunas expectativas sobre "cómo debería ser un valor atípico". Hay aproximadamente tres tipos de valores atípicos, que se resumen a continuación:
Los valores atípicos globales (también llamados valores atípicos puntuales) son observaciones únicas e independientes que se desvían de todas las demás observaciones. Cuando alguien habla de "valores atípicos", generalmente se refiere al valor atípico global.
Los valores atípicos contextuales ocurren cuando una observación particular no encaja en un contexto específico. Un contexto puede presentarse en una distribución bimodal o multimodal, y un valor atípico se desvía dentro del contexto. Por ejemplo, las temperaturas por debajo de 0 son normales en invierno pero son inusuales en verano y se denominan valores atípicos. Además de las series temporales y los datos estacionales, otras aplicaciones conocidas se encuentran en datos de sensores y operaciones de seguridad.
Los valores atípicos colectivos (o valores atípicos de grupo) son un grupo de instancias similares/relacionadas con un comportamiento inusual en comparación con el resto del conjunto de datos. El grupo de valores atípicos puede formar una distribución bimodal o multimodal porque a menudo indican un tipo de problema diferente al de los valores atípicos individuales, como un error de procesamiento por lotes o un problema sistémico en el proceso de generación de datos. Tenga en cuenta que la detección de valores atípicos colectivos normalmente requiere un enfoque diferente al de la detección de valores atípicos individuales.
Una parte más que debe discutirse antes de que podamos comenzar a modelar valores atípicos es la parte del conjunto de datos. Desde la perspectiva de un conjunto de datos, los valores atípicos se pueden detectar en función de una sola característica (univariante) o en función de múltiples características por observación multivariante). Sigue leyendo porque la siguiente sección trata sobre el análisis univariante y multivariante.
Los valores atípicos se pueden modelar de forma univariante o multivariante. Un enfoque de modelado para la detección de cualquier tipo de valor atípico tiene dos sabores principales; análisis univariante y multivariante (Figura 2). Me centraré en la detección de valores atípicos para variables aleatorias univariadas, pero no antes de describir brevemente las diferencias:
El enfoque univariante es cuando la muestra/observación se marca como un valor atípico usando una variable a la vez, es decir, la edad de una persona, el peso o una sola variable en los datos de series de tiempo. El análisis de la distribución de datos en tales casos es muy adecuado para la detección de valores atípicos.
El enfoque multivariante es cuando la muestra/observaciones contienen múltiples características que pueden analizarse conjuntamente, como la edad, el peso y la altura. Es muy adecuado para detectar valores atípicos con características que tienen relaciones (no) lineales o donde la distribución de valores en cada variable es (altamente) sesgada. En estos casos, el enfoque univariante puede no ser tan efectivo, ya que no tiene en cuenta las relaciones entre variables.
Detección de valores atípicos en variables univariadas mediante ajuste de distribución. Existen varias formas (no) paramétricas para la detección de valores atípicos en conjuntos de datos univariados, como puntajes Z, vallas de Tukey y enfoques basados en la densidad, entre otros. El tema común entre los métodos es que se modela la distribución subyacente. Por lo tanto, la biblioteca distfit es adecuada para la detección de valores atípicos, ya que puede determinar la función de densidad de probabilidad (PDF) para variables aleatorias univariadas, pero también puede modelar conjuntos de datos univariados de manera no paramétrica utilizando percentiles o cuantiles. Además, se puede utilizar para modelar anomalías o novedades en cualquiera de las tres categorías; valores atípicos globales, contextuales o colectivos. Consulte este blog para obtener información más detallada sobre el ajuste de distribución utilizando la biblioteca distfit. El enfoque de modelado se puede resumir de la siguiente manera:
Calcule el ajuste de su variable aleatoria en varios archivos PDF, luego clasifique los archivos PDF usando la prueba de bondad de ajuste y evalúe con un enfoque de arranque. Tenga en cuenta que también se pueden utilizar enfoques no paramétricos con cuantiles o percentiles. Inspeccione visualmente el histograma, los PDF, los CDF y el gráfico Cuantil-Cuantil (QQ).
Elija el mejor modelo según los pasos 1 y 2, pero también asegúrese de que las propiedades del modelo (no) paramétrico (por ejemplo, el PDF) coincidan con el caso de uso. Elegir el mejor modelo no es solo una cuestión estadística; también es una decisión de modelado. Realice predicciones sobre nuevas muestras no vistas utilizando el modelo (no) paramétrico como el PDF.
Comencemos con un ejemplo simple e intuitivo para demostrar el funcionamiento de la detección de novedad para variables univariadas mediante el ajuste de distribución y la prueba de hipótesis. En este ejemplo, nuestro objetivo es seguir un enfoque novedoso para la detección de valores atípicos globales, es decir, los datos no contienen observaciones que se desvíen de lo normal/esperado. Esto significa que, en algún momento, debemos incluir cuidadosamente el conocimiento del dominio para establecer los límites de cómo se ve un valor atípico.
Supongamos que tenemos medidas de 10.000 alturas humanas. Generemos datos normales aleatorios con media = 163 y std = 10 que representan nuestras medidas de altura humana. Esperamos una curva en forma de campana que contenga dos colas; aquellos con alturas más pequeñas y más grandes que el promedio. Tenga en cuenta que, debido al componente estocástico, los resultados pueden diferir ligeramente al repetir el experimento.
import numpy as np
from distfit import distfit
from matplotlib import pyplot as plt
X = np.random.normal(163, 10, 10000)
Antes de que podamos detectar valores atípicos, debemos ajustar una distribución (PDF) sobre cuál es el comportamiento normal/esperado para la altura humana. La biblioteca distfit puede albergar hasta 89 distribuciones teóricas. Limitaré la búsqueda solo a funciones de densidad de probabilidad comunes/populares, ya que esperamos fácilmente una curva en forma de campana (consulte la siguiente sección de código).
dfit = distfit(distr='popular', n_boots=100)
results = dfit.fit_transform(X)
dfit.plot_summary(n_top=10)
plt.show()
[distfit] >INFO> fit [distfit] >INFO> transform [distfit] >INFO> [norm ] [1.12 sec] [RSS: 5.7328e-05] [loc=163.028 scale=10.011] [distfit] >INFO> [expon ] [0.90 sec] [RSS: 0.0173364] [loc=123.632 scale=39.396] [distfit] >INFO> [pareto ] [56.1 sec] [RSS: 0.0192586] [loc=-0.314 scale=123.945] [distfit] >INFO> [dweibull ] [23.0 sec] [RSS: 0.000238248] [loc=163.293 scale=8.542] [distfit] >INFO> [t ] [51.8 sec] [RSS: 5.7409e-05] [loc=163.016 scale=9.998] [distfit] >INFO> [genextreme] [173. sec] [RSS: 0.0470114] [loc=203.560 scale=6.765] [distfit] >INFO> [gamma ] [33.9 sec] [RSS: 6.05656e-05] [loc=-674.146 scale=0.120] [distfit] >INFO> [lognorm ] [84.5 sec] [RSS: 0.000570502] [loc=106.234 scale=55.695] [distfit] >INFO> [beta ] [63.7 sec] [RSS: 5.58594e-05] [loc=-120.706 scale=492.311] [distfit] >INFO> [uniform ] [0.90 sec] [RSS: 0.012937] [loc=123.632 scale=81.663] [distfit] >INFO> [loggamma ] [74.7 sec] [RSS: 5.53155e-05] [loc=-1658.818 scale=274.997] [distfit] >INFO> Compute confidence intervals [parametric] [distfit] >INFO> Ploting Summary. [distfit] >INFO> Bootstrap results are included..
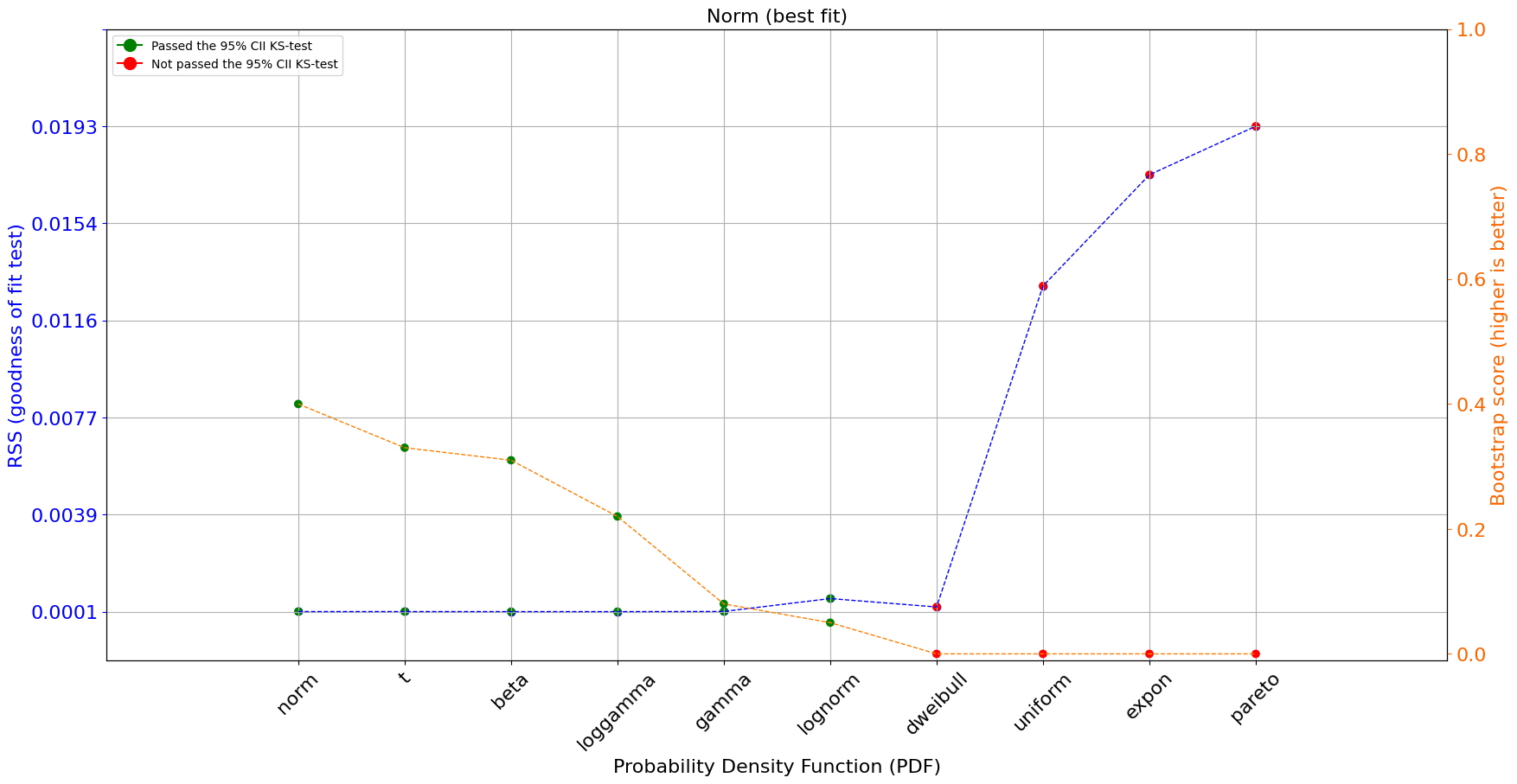
El loggamma PDF se detecta como el mejor ajuste para la altura humana de acuerdo con la estadística de prueba de bondad de ajuste (RSS) y el enfoque de arranque. Tenga en cuenta que el enfoque de arranque evalúa si hubo sobreajuste para los archivos PDF. La puntuación de arranque oscila entre [0, 1] y representa la proporción de ajuste-éxito en el número de arranques (n_bootst=100) para el PDF. También se puede ver en la Figura 3 que, además del PDF loggamma, también se detectan muchos otros PDF con una suma residual de cuadrados baja, es decir, Beta, Gamma, Normal, distribución T, Loggamma, valor extremo generalizado y Weibull. distribución. Sin embargo, solo cinco archivos PDF aprobaron el método de arranque.
Una mejor práctica es inspeccionar visualmente el ajuste de la distribución. La biblioteca distfit contiene funcionalidades integradas para el trazado, como el histograma combinado con PDF/CDF pero también gráficos QQ. La trama se puede crear de la siguiente manera:
fig, ax = plt.subplots(1, 2, figsize=(20, 8))
dfit.plot(chart='PDF', n_top=1, ax=ax[0]);
dfit.plot(chart='CDF', n_top=10, ax=ax[1])
plt.show()
[distfit] >INFO> Create PDF plot for the parametric method. [distfit] >INFO> Estimated distribution: Norm(loc:163.027510, scale:10.011438) [distfit] >INFO> Create CDF plot for the parametric method. [distfit] >INFO> Ploting CDF
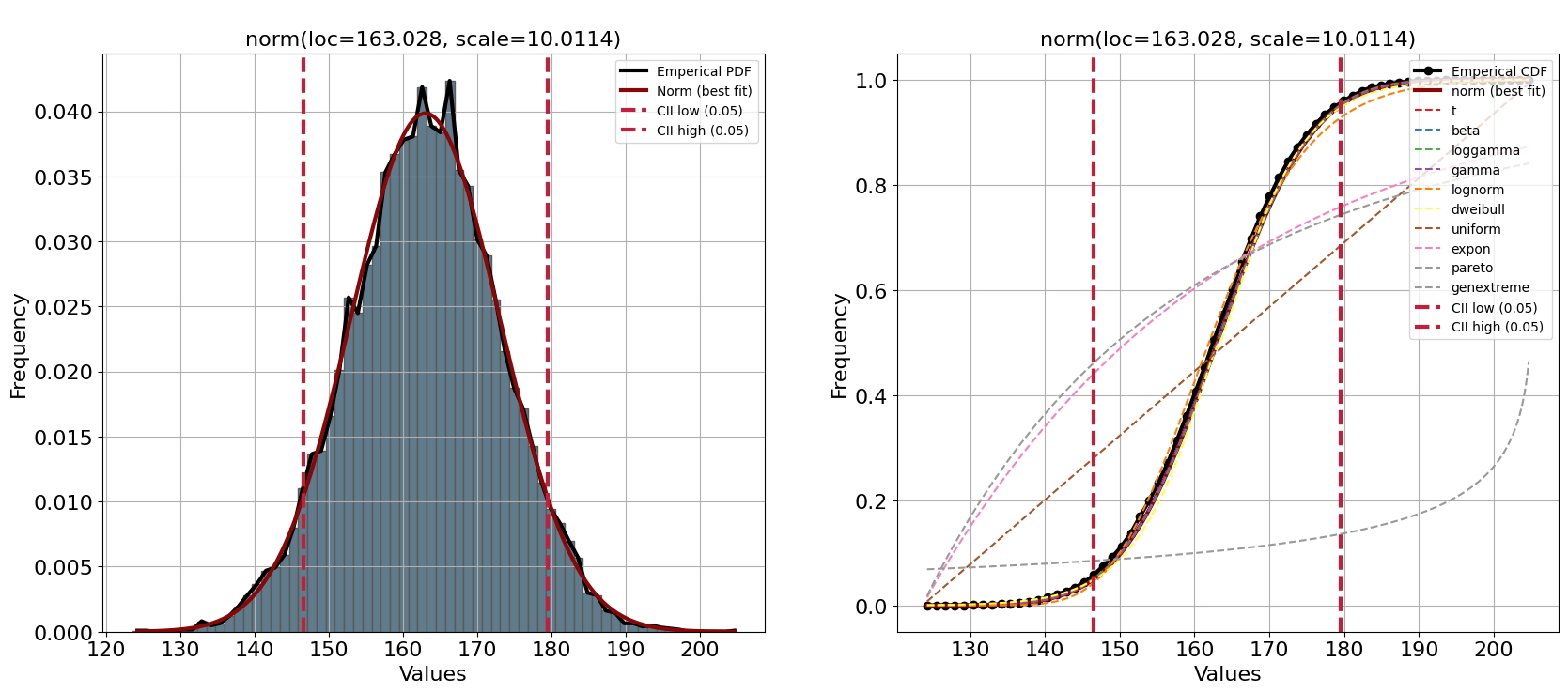
Una inspección visual confirma la bondad de las puntuaciones de ajuste de los PDF mejor clasificados. Sin embargo, hay una excepción, la distribución de Weibull (línea amarilla en la Figura 4) parece tener dos picos. En otras palabras, aunque el RSS es bajo, una inspección visual no muestra un buen ajuste para nuestra variable aleatoria. Tenga en cuenta que el enfoque de arranque excluyó fácilmente la distribución de Weibull y ahora sabemos por qué.
El último paso puede ser el paso más desafiante porque todavía hay cinco distribuciones candidatas que obtuvieron muy buenos puntajes en la prueba de bondad de ajuste, el enfoque de arranque y la inspección visual. Ahora deberíamos decidir qué PDF coincide mejor con sus propiedades fundamentales para modelar la altura humana. Profundizaré paso a paso en las propiedades de las principales distribuciones candidatas con respecto a nuestro caso de uso de modelar la altura humana.
La distribución Normal es una opción típica, pero es importante tener en cuenta que la suposición de normalidad para la estatura humana puede no ser válida en todas las poblaciones. No tiene colas pesadas y, por lo tanto, es posible que no capture muy bien los valores atípicos.
La distribución T de Student se usa a menudo como una alternativa a la distribución normal cuando el tamaño de la muestra es pequeño o se desconoce la varianza de la población. Tiene colas más pesadas que la distribución normal, lo que puede capturar mejor la presencia de valores atípicos o sesgos en los datos. En caso de tamaños de muestra bajos, esta distribución podría haber sido una opción, pero a medida que aumenta el tamaño de la muestra, la distribución t se acerca a la distribución normal.
La distribución Gamma es una distribución continua que a menudo se usa para modelar datos que tienen un sesgo positivo, lo que significa que hay una cola larga de valores altos. La altura humana puede tener un sesgo positivo debido a la presencia de valores atípicos, como individuos muy altos. Sin embargo, el enfoque bootstrap mostró un mal ajuste.
La distribución Log-gamma tiene una forma sesgada, similar a la distribución gamma, pero con colas más pesadas. Modela el registro de los valores, lo que lo hace más apropiado para usar cuando los datos tienen una gran cantidad de valores altos.
La distribución Beta generalmente se usa para modelar proporciones o tasas [9], en lugar de variables continuas como en nuestro caso de uso para la altura. Habría sido una elección adecuada si la altura se dividiera por un valor de referencia, como la mediana de la altura. Entonces, a pesar de que obtiene la mejor puntuación en la prueba de bondad de ajuste y confirmamos un buen ajuste mediante una inspección visual, no sería mi primera opción.
La distribución de valores extremos generalizados (GEV) se puede utilizar para modelar la distribución de valores extremos en una población, como los valores máximos o mínimos. También permite colas pesadas que pueden capturar la presencia de valores atípicos o sesgos en los datos. Sin embargo, normalmente se usa para modelar la distribución de valores extremos [10], en lugar de la distribución general de una variable continua como la altura humana.
Es posible que la distribución de Dweibull no sea la mejor opción para esta pregunta de investigación, ya que generalmente se usa para modelar datos que tienen una tendencia monotónica creciente o decreciente, como los datos de tiempo hasta falla o tiempo hasta evento. Los datos de altura humana pueden no tener una tendencia monótona clara. La inspección visual del gráfico PDF/CDF/QQ tampoco mostró una buena incidencia
En resumen, la distribución loggamma puede ser la mejor opción en este caso de uso particular después de considerar la prueba de bondad de ajuste, el enfoque de arranque, la inspección visual y ahora también en función de las propiedades de PDF relacionadas con la pregunta de investigación. Tenga en cuenta que podemos especificar fácilmente la distribución loggamma y volver a ajustar los datos de entrada (consulte la sección de códigos) si es necesario (consulte la sección de códigos).
dfit = distfit(distr='loggamma', alpha=0.01, bound='both')
results = dfit.fit_transform(X)
print(dfit.model)
# dfit.save('./human_height_model.pkl')
[distfit] >INFO> fit [distfit] >INFO> transform [distfit] >INFO> [loggamma] [0.53 sec] [RSS: 5.53155e-05] [loc=-1658.818 scale=274.997] [distfit] >INFO> Compute confidence intervals [parametric]
{'name': 'loggamma', 'score': 5.531547878947298e-05, 'loc': -1658.8175767223656,
'scale': 274.9974343225563, 'arg': (754.1649974963748,),
'params': (754.1649974963748, -1658.8175767223656, 274.9974343225563),
'model': <scipy.stats._distn_infrastructure.rv_frozen object at 0x0000017CF3114048>,
'bootstrap_score': 0, 'bootstrap_pass': None, 'color': '#e41a1c',
'CII_min_alpha': 139.4535555539385,
'CII_max_alpha': 186.0622211891416}
Con el modelo ajustado podemos evaluar la importancia de las muestras nuevas (no vistas) y detectar si se desvían de lo que es normal/esperado (los inliers). Las predicciones se realizan sobre la función de densidad de probabilidad teórica, lo que la hace liviana, rápida y explicable. Los intervalos de confianza para el PDF se establecen mediante el parámetro alfa. Esta es la parte donde se requiere conocimiento del dominio porque no hay valores atípicos conocidos en nuestro conjunto de datos presente. En este caso, establecí el intervalo de confianza (CII) alfa = 0,01, lo que da como resultado un límite mínimo de 139,8 cm y un límite máximo de 185,8 cm. El valor predeterminado es que se analizan ambas colas, pero esto se puede cambiar usando el parámetro de límite (consulte la sección de código anterior).
Podemos usar la función de predicción para hacer nuevas predicciones sobre nuevas muestras no vistas y crear la gráfica con los resultados de la predicción (Figura 5). Tenga en cuenta que la importancia se corrige para múltiples pruebas: multtest='fdr_bh'. Por lo tanto, los valores atípicos pueden ubicarse fuera del intervalo de confianza pero no marcarse como significativos.
y = [130, 160, 200]
results = dfit.predict(y, alpha=0.01, multtest='fdr_bh', todf=True)
results['df']
plt.figure();
fig, ax = plt.subplots(1, 2, figsize=(20, 8))
dfit.plot(chart='PDF', ax=ax[0]);
dfit.plot(chart='CDF', ax=ax[1])
plt.show()
[distfit] >INFO> Alpha is set to [0.01] [distfit] >INFO> Compute confidence intervals [parametric] [distfit] >INFO> Compute significance for 3 samples. [distfit] >INFO> Multiple test correction method applied: [fdr_bh]. [distfit] >INFO> Create PDF plot for the parametric method. [distfit] >INFO> Mark 2 significant regions [distfit] >INFO> Estimated distribution: Loggamma(loc:-1658.817577, scale:274.997434) [distfit] >INFO> Create CDF plot for the parametric method. [distfit] >INFO> Ploting CDF [distfit] >INFO> Mark 2 significant regions
<Figure size 640x480 with 0 Axes>
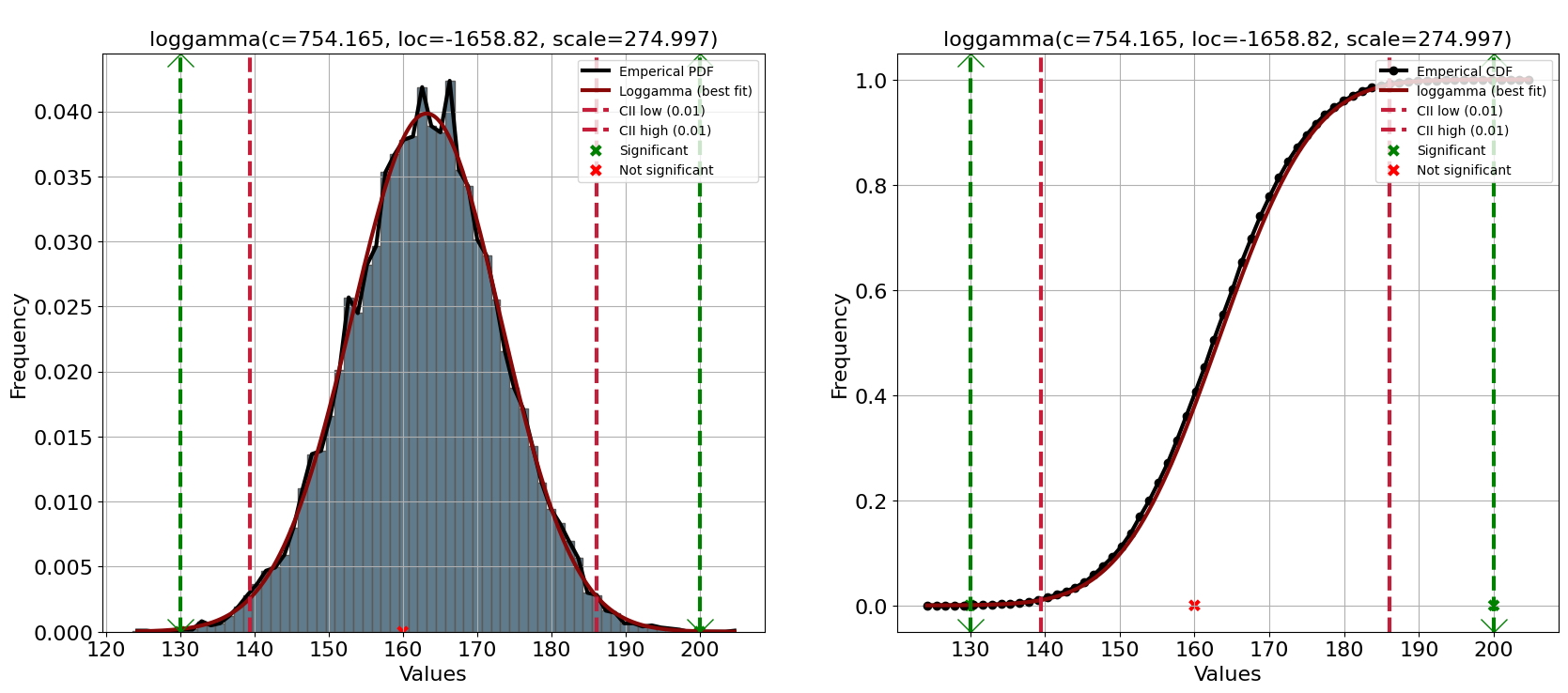
Los resultados de las predicciones se almacenan en resultados y contienen varias columnas: y, y_proba, y_pred y P . La P representa los valores p sin procesar e y_proba son las probabilidades después de múltiples correcciones de prueba (predeterminado: fdr_bh). Tenga en cuenta que se devuelve un marco de datos cuando se usa el parámetro todf=True. Dos observaciones tienen una probabilidad alfa <0,01 y se marcan como significativas hacia arriba o hacia abajo.
Hasta ahora hemos visto cómo ajustar un modelo y detectar valores atípicos globales para la detección de novedades. Aquí usaremos datos del mundo real para la detección de anomalías. El uso de datos del mundo real suele ser mucho más desafiante para trabajar. Para demostrar esto, descargaré el conjunto de datos del precio spot del gas natural de Thomson Reuters [7], que es un conjunto de datos de código abierto y disponible gratuitamente [8]. Después de descargar, importar y eliminar valores nan, hay 6555 puntos de datos en 27 años.
dfit = distfit()
df = dfit.import_example(data='gas_spot_price')
df.head()
[distfit] >INFO> Downloading and processing [gas_spot_price] from github source.
| price | |
|---|---|
| date | |
| 2023-02-07 | 2.35 |
| 2023-02-06 | 2.17 |
| 2023-02-03 | 2.40 |
| 2023-02-02 | 2.67 |
| 2023-02-01 | 2.65 |
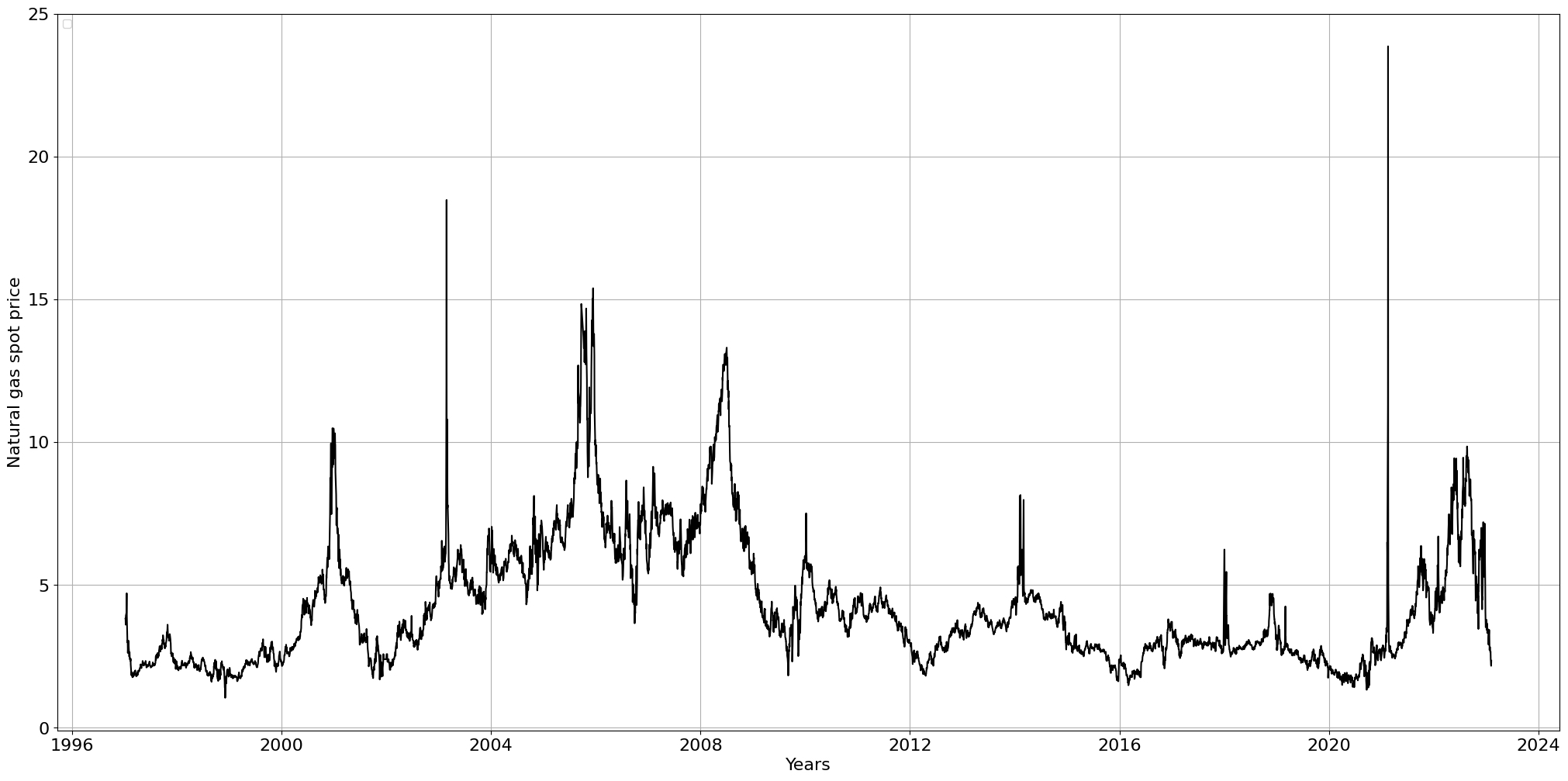
Para inspeccionar visualmente los datos, podemos crear un diagrama de líneas del precio spot del gas natural para ver si hay tendencias obvias u otros asuntos relevantes. Se puede ver que 2003 y 2021 contienen dos picos importantes (que apuntan hacia valores atípicos globales). Además, las acciones del precio parecen tener un movimiento natural con máximos y mínimos locales. Con base en este gráfico de líneas, podemos construir una intuición de la distribución esperada. El precio se mueve principalmente en el rango [2, 5] pero con algunos años excepcionales de 2003 a 2009, donde el rango estuvo más entre [6, 9].
dfit.lineplot(df, xlabel='Years', ylabel='Natural gas spot price', grid=True)
plt.show()
[distfit] >INFO> Dataframe detected. Labels are derived from the index and the data is flattened. No artists with labels found to put in legend. Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
Usemos distfit para investigar más a fondo la distribución de datos y determinar el PDF adjunto. El espacio de búsqueda se establece en todos los archivos PDF disponibles y el enfoque de arranque se establece en 100 para evaluar el sobreajuste de los archivos PDF.
# dfit = distfit(distr='full', n_boots=100)
dfit = distfit(distr='popular', n_boots=100)
results = dfit.fit_transform(df['price'].values)
fig, ax = plt.subplots(1,2, figsize=(25, 10))
dfit.plot(chart='PDF', n_top=10, ax=ax[0])
dfit.plot(chart='CDF', n_top=10, ax=ax[1])
plt.show()
[distfit] >INFO> fit [distfit] >INFO> transform [distfit] >INFO> [norm ] [1.06 sec] [RSS: 0.169681] [loc=4.235 scale=2.195] [distfit] >INFO> [expon ] [1.00 sec] [RSS: 0.257492] [loc=1.050 scale=3.185] [distfit] >INFO> [pareto ] [27.6 sec] [RSS: 0.739523] [loc=0.001 scale=1.049] [distfit] >INFO> [dweibull ] [19.3 sec] [RSS: 0.124167] [loc=3.695 scale=1.675] [distfit] >INFO> [t ] [37.0 sec] [RSS: 0.131213] [loc=3.779 scale=1.566] [distfit] >INFO> [genextreme] [65.2 sec] [RSS: 0.0344589] [loc=3.091 scale=1.243] [distfit] >INFO> [gamma ] [11.2 sec] [RSS: 0.0545076] [loc=1.047 scale=1.288] [distfit] >INFO> [lognorm ] [55.4 sec] [RSS: 0.0316565] [loc=0.994 scale=2.636] [distfit] >INFO> [beta ] [76.9 sec] [RSS: 0.0545361] [loc=1.047 scale=25085.315] [distfit] >INFO> [uniform ] [1.05 sec] [RSS: 0.525032] [loc=1.050 scale=22.810] [distfit] >INFO> [loggamma ] [49.2 sec] [RSS: 0.172759] [loc=-637.212 scale=87.927] [distfit] >INFO> Compute confidence intervals [parametric] [distfit] >INFO> Create PDF plot for the parametric method. [distfit] >INFO> Estimated distribution: Lognorm(loc:0.994065, scale:2.636157) [distfit] >INFO> Create CDF plot for the parametric method. [distfit] >INFO> Ploting CDF
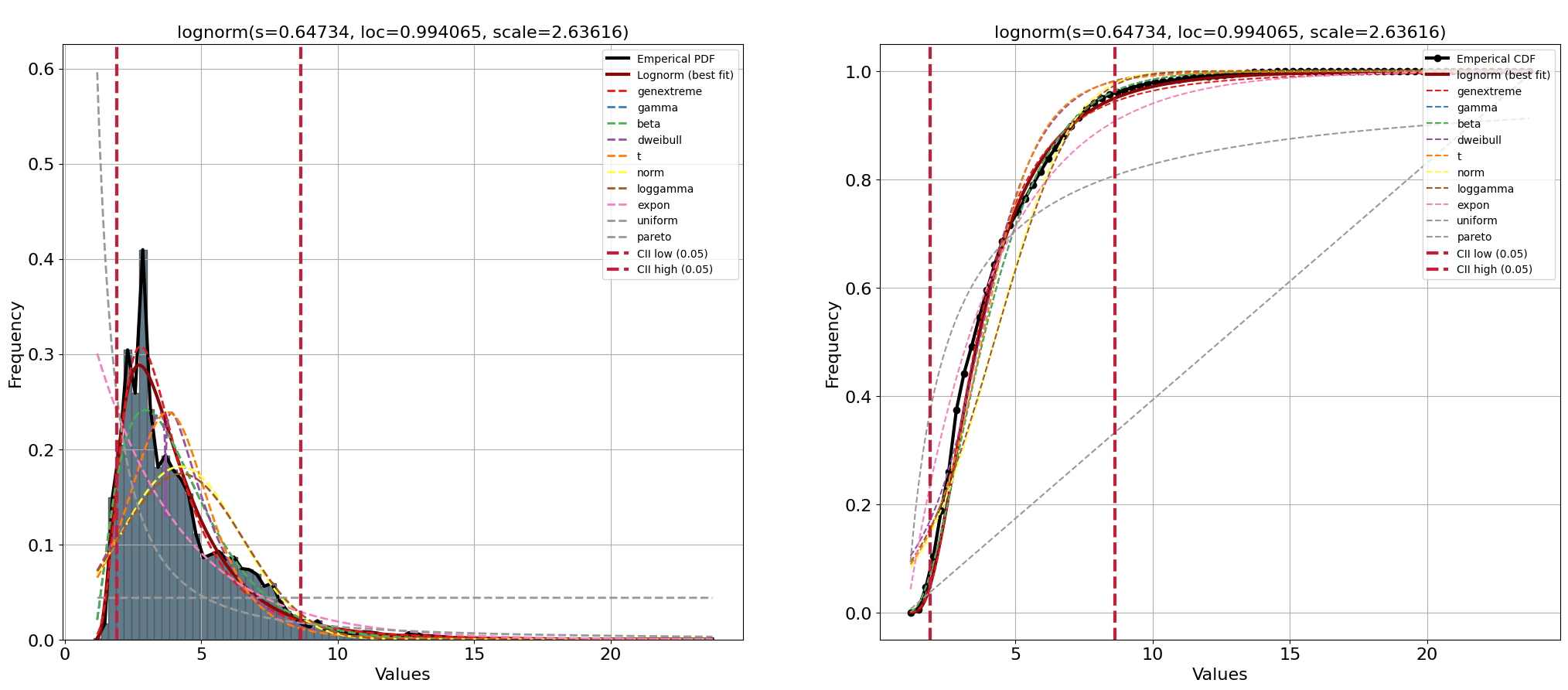
La PDF que mejor se ajusta es Johnsonsb, pero cuando trazamos las distribuciones de datos empíricos, la PDF (línea roja) no sigue con precisión los datos empíricos. En general, podemos confirmar que la mayoría de los puntos de datos están ubicados en el rango [2, 5] (aquí es donde está el pico de la distribución) y que hay un segundo pico más pequeño en la distribución con acciones de precio alrededor del valor 6 Este es también el punto en el que el PDF no se ajusta sin problemas a los datos empíricos y provoca algunos rebasamientos y rebasamientos. Con el gráfico de resumen y el gráfico QQ, podemos investigar el ajuste aún mejor. Vamos a crear estos dos gráficos con las siguientes líneas de código:
fig, ax = plt.subplots(1,2, figsize=(25, 10))
dfit.plot_summary(ax=ax[0])
dfit.qqplot(df['price'].values, n_top=10, ax=ax[1])
plt.show()
[distfit] >INFO> Ploting Summary. [distfit] >INFO> Bootstrap results are included..
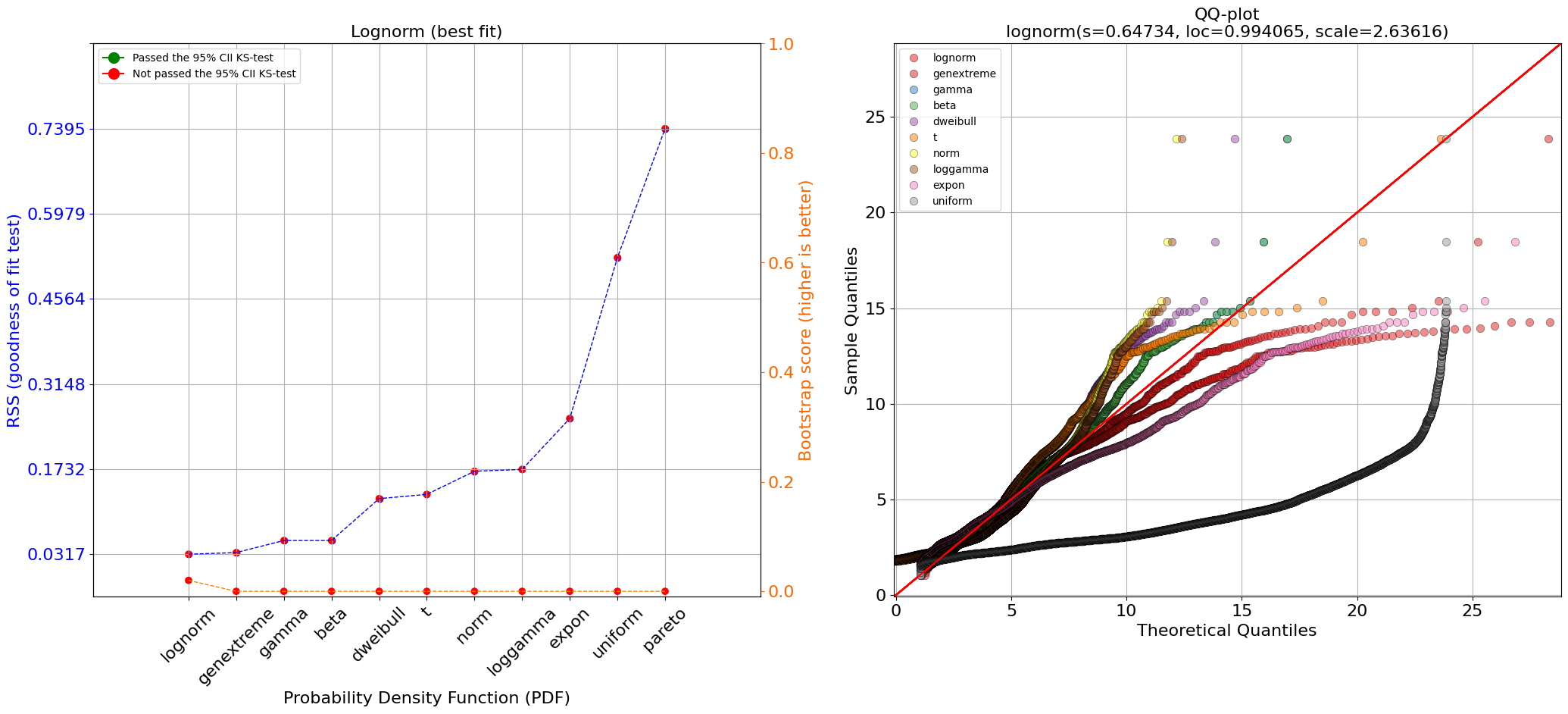
Es interesante ver en la gráfica de resumen que la prueba de bondad de ajuste mostró buenos resultados (puntuación baja) entre todas las distribuciones superiores. Sin embargo, cuando observamos los resultados del enfoque bootstrap, muestra que todas, excepto una distribución, están sobreajustadas (Figura 8A, línea naranja). Esto no es del todo inesperado porque ya notamos un exceso y un defecto. El gráfico QQ confirma que las distribuciones ajustadas se desvían mucho de los datos empíricos. Solo la distribución de Johnsonsb mostró un buen ajuste (límite).
Continuaremos usando la distribución de Johnsonsb y la función de predicción para la detección de valores atípicos. Ya sabemos que nuestro conjunto de datos contiene valores atípicos ya que seguimos el enfoque de anomalías, es decir, la distribución se ajusta a los valores internos y las observaciones que ahora quedan fuera de los intervalos de confianza se pueden marcar como valores atípicos potenciales. Con la función de predicción y el diagrama de líneas podemos detectar y trazar los valores atípicos. En la Figura 9 se puede ver que se detectan los valores atípicos globales pero también algunos valores atípicos contextuales, a pesar de que no lo modelamos explícitamente. Las barras rojas son los valores atípicos subrepresentados y las barras verdes son los valores atípicos sobrerrepresentados. El parámetro alfa se puede configurar para ajustar los intervalos de confianza.
dfit.predict(df['price'].values, alpha=0.05, multtest=None)
dfit.lineplot(df['price'], labels=df.index)
[distfit] >INFO> Alpha is set to [0.05] [distfit] >INFO> Compute confidence intervals [parametric] [distfit] >INFO> Compute significance for 6555 samples.
(<Figure size 2500x1200 with 1 Axes>,
<AxesSubplot:title={'center':'\nlognorm(s=0.64734, loc=0.994065, scale=2.63616)'},
xlabel='x-axes', ylabel='y-axes'>)
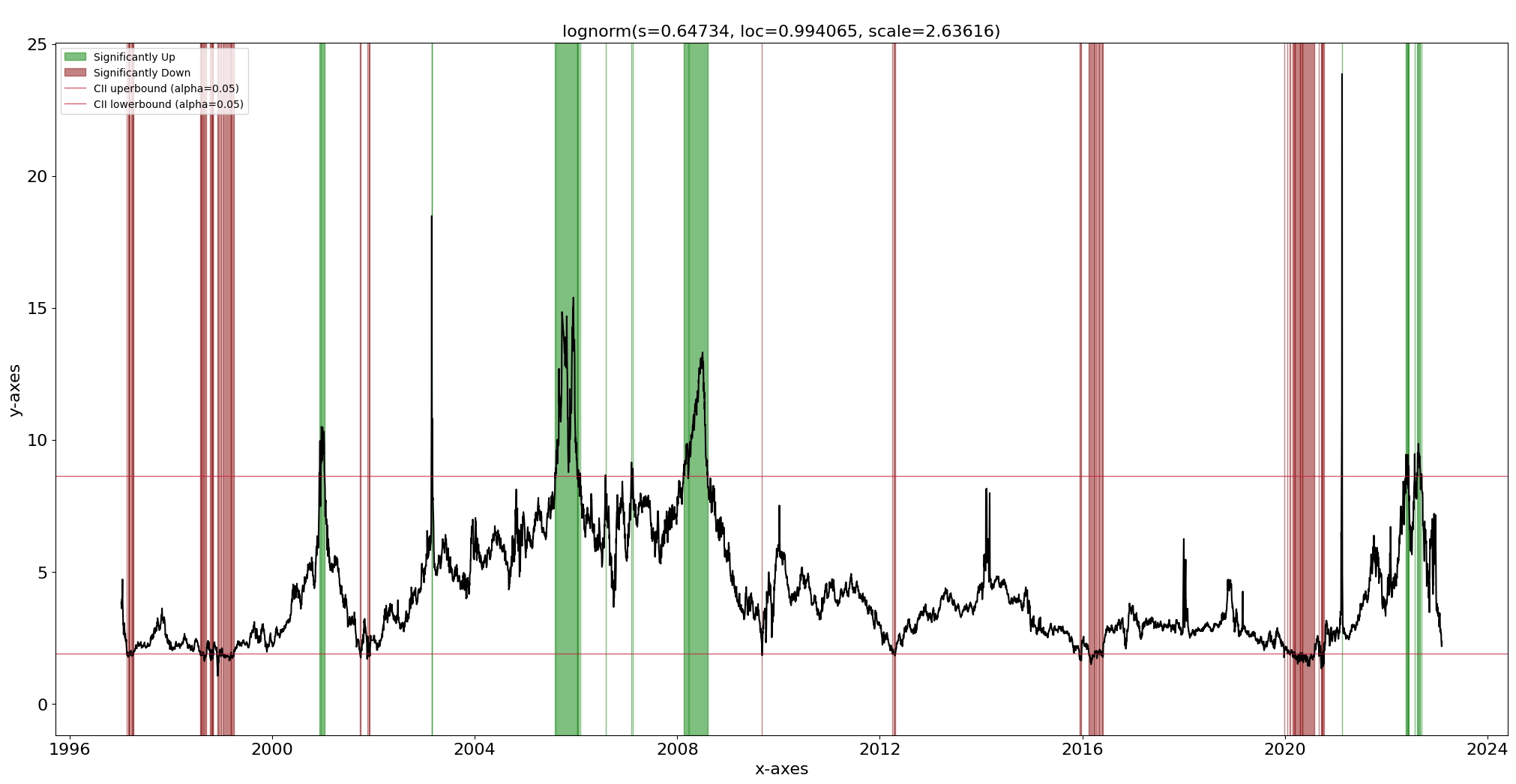
Trazado de valores atípicos después de ajustar la distribución y hacer predicciones. Las barras verdes son valores atípicos fuera del límite superior del 95% CII. Las barras rojas son valores atípicos fuera del límite inferior del 95% CII.
Describimos las diferencias entre la detección de anomalías y novedades y cómo crear un modelo mediante el ajuste de distribución. Con la biblioteca distfit, se pueden evaluar y seleccionar 89 distribuciones teóricas y se pueden hacer predicciones sobre nuevas muestras no vistas. Con un ejemplo práctico y un conjunto de datos del mundo real, mostré cómo determinar el PDF más adecuado. Tenga en cuenta que puede ocurrir que ninguna de las distribuciones teóricas conocidas coincida significativamente. En ese caso, la biblioteca distfit también tiene la opción de ajuste no paramétrico utilizando percentiles o cuantiles. Se puede encontrar más información en mi blog anterior sobre ajuste de distribución [6]. Es importante tener en cuenta que la detección de valores atípicos es una tarea desafiante, ya que la definición de lo que es normal o esperado puede ser subjetiva y puede diferir según la aplicación. Además, los valores atípicos pueden deberse a errores de medición, errores de datos o fluctuaciones naturales, por lo que es importante considerar detenidamente la causa subyacente de la desviación antes de sacar conclusiones.