Volver al Inicio

Anterior Siguiente

03 de Marzo del 2022 | Jhonatan Montilla

Análisis de Componenetes Principales (PCA)

Hay mucho más en el análisis de componentes principales, más allá del contenido de este artículo, por lo que la única manera de apreciar verdaderamente la belleza de este es experimentarlo por usted mismo. Por lo tanto, vamos a compartir algunos fragmentos de código aquí para cualquiera que quiera probarlo.

Primero se cargaran las librerías necesarias y crearemos algunos datos sintéticos para las pruebas.

import pandas as pd
import numpy as np

from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

import matplotlib.pyplot as plt
import seaborn as sns
import plotly.express as px

# Cree una matriz con 3 clústeres en 3 dimensiones
X, y = make_blobs(n_samples = 1000,
                  centers = 3,
                  n_features = 3,
                  random_state = 0,
                  cluster_std = [1,2,3],
                  center_box = (10,65))

# Estandarizar los datos
X = StandardScaler().fit_transform(X)

# Preparar la matriz en un DataFrame
col_name = ['x' + str(idx) for idx in range(0, X.shape[1])]
df = pd.DataFrame(X, columns = col_name)
df['cluster_label'] = y

df.head()

	x0	x1	x2	cluster_label
0	-0.366353	1.022466	1.166899	2
1	-1.179214	1.318905	1.047407	2
2	0.346441	-1.360488	-0.417740	1
3	0.507115	0.055279	-0.890964	0
4	-0.185192	0.937566	0.930304	2

# Visualiza nuestros datos
colors = px.colors.sequential.Plasma
colors[0], colors[1], colors[2] = ['red', 'green', 'blue']
fig = px.scatter_3d(df,
                    x ='x0',
                    y = 'x1',
                    z = 'x2',
                    color = df['cluster_label'].astype(str),
                    color_discrete_sequence = colors,
                    height = 500,
                    width = 1000)
fig.update_layout(showlegend = False,
                  scene_camera = dict(up = dict(x = 0,
                                                y = 0,
                                                z = 1), 
                                    center = dict(x = 0,
                                                  y = 0,
                                                  z = -0.1),
                                    eye = dict(x = 1.5,
                                               y = -1.4,
                                               z = 0.5)),
                  margin = dict(l = 0,
                                r = 0,
                                b = 0,
                                t = 0),
                  scene=dict(xaxis = dict(backgroundcolor = 'white',
                                        color = 'black',
                                        gridcolor = '#f0f0f0',
                                        title_font = dict(size=10),
                                        tickfont = dict(size=10)),
                             yaxis = dict(backgroundcolor = 'white',
                                        color = 'black',
                                        gridcolor = '#f0f0f0',
                                        title_font = dict(size = 10),
                                        tickfont = dict(size = 10)),
                             zaxis = dict(backgroundcolor = 'lightgrey',
                                        color = 'black', 
                                        gridcolor = '#f0f0f0',
                                        title_font = dict(size = 10),
                                        tickfont = dict(size = 10))))
fig.update_traces(marker = dict(size = 3,
                                line = dict(color = 'black',
                                            width = 0.1)))
fig.show()

Los datos parecen estar listos para en análisis con PCA. Vamos a intentar reducir su dimensionalidad, afortunadamente para nosotros, la librería de Python, Sklearn hace que el análisis de componentes principales sea muy fácil de ejecutar, aunque tome varias palabras explicar el análisis con PCA, con dicha librería solo necesitamos 3 líneas para ejecutarlo.

# Realizar PCA (sin límites en n_components)
pca = PCA()
_ = pca.fit_transform(df[col_name])
PC_components = np.arange(pca.n_components_) + 1

Hay un par de partes móviles aquí. Cuando ajustamos nuestros datos a la función PCA de Sklearn, hace todo el trabajo pesado para devolvernos un modelo PCA y los datos transformados.

El modelo nos da acceso a multitud de atributos como valores propios, vectores propios, media de los datos originales, varianza explicada y la lista continúa. Estos son increíblemente perspicaces si queremos entender qué ha hecho el PCA con nuestros datos.

Un atributo que nos gustaría resaltar es el pca.explained_varianceratio que nos dice la proporción de varianza explicada por cada componente principal. Podríamos visualizar esto con un Screen Plot.

_ = sns.set(style = 'whitegrid',
            font_scale = 1.2)
fig, ax = plt.subplots(figsize = (10, 7))
_ = sns.barplot(x = PC_components,
                y = pca.explained_variance_ratio_,
                color = 'b')
_ = sns.lineplot(x = PC_components-1,
                 y = np.cumsum(pca.explained_variance_ratio_),
                 color = 'black',
                 linestyle = '-',
                 linewidth = 2,
                 marker = 'o',
                 markersize = 8)
plt.title('Scree Plot')
plt.xlabel('N-th Principal Component')
plt.ylabel('Variance Explained')
plt.ylim(0, 1)
plt.show()

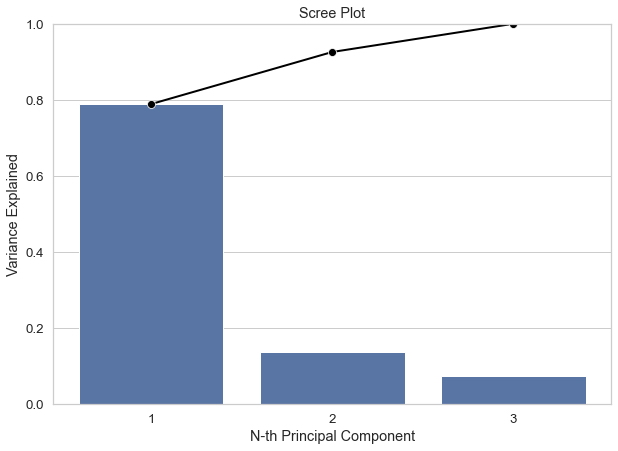
El gráfico nos informa que usar 2 componentes principales en lugar de 3 está bien porque éstos pueden capturar más del 90% de la varianza.

Además de esto, también podemos ver las combinaciones de variables que creó cada componente principal con pca.components_**2. Vamos a crear un mapa de calor para mostrar esto.

# Peso de la característica
_ = sns.heatmap(pca.components_**2,
                 yticklabels = ["PCA" + str(x) for x in range(1,pca.n_components_+1)],
                 xticklabels = list(col_name),
                 annot = True,
                 fmt = '.2f',
                 square = True,
                 linewidths = 0.05,
                 cbar_kws = {"orientation": "horizontal"})

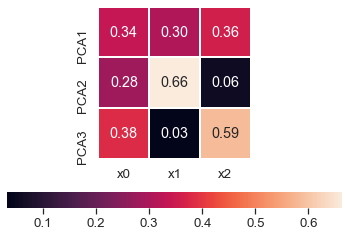
En nuestro ejemplo, podemos observar que PCA1 está compuesto por un 34% de x0, un 30% de x1 y un 36% de x2. PCA2 está dominado principalmente por x1.

Sklearn pone a disposición muchos más atributos útiles. Para aquellos que estén interesados, recomendamos echar un vistazo a la sección de atributos de PCA en la documentación de Sklearn.

Ahora que entendemos un poco mejor los componentes principales, podemos tomar una decisión final sobre la cantidad de componentes principales que queremos conservar. En este caso, creemos que 2 componentes principales son suficientes.

Entonces, podemos volver a ejecutar el modelo PCA, pero esta vez con el argumento n_components = 2, que le dice a PCA que conserve solo los 2 componentes principales principales para nuestro caso de estudio.

# Realizar PCA (Elija n_components para mantener)
pca = PCA(n_components=2)
pca_array = pca.fit_transform(df)

# Convertir de nuevo a DataFrame para facilitar la lectura
df_pca = pd.DataFrame(data=pca_array)
df_pca.columns = ['PC' + str(col+1) for col in df_pca.columns.values]
df_pca['label'] = y

df_pca.head()

	PC1	PC2	label
0	1.750435	-0.041716	2
1	2.255957	-0.226133	2
2	-1.058243	0.998596	1
3	-1.165212	-0.799110	0
4	1.478118	-0.034766	2

Esto nos devolverá un DataFrame con los dos primeros componentes principales. Finalmente, podemos trazar un diagrama de dispersión para visualizar nuestros datos.

# Componente principal de la trama
_ = sns.set(style = 'ticks',
            font_scale = 1.2)
fig, ax = plt.subplots(figsize = (10, 7))
_ = sns.scatterplot(data = df_pca,
                    x = 'PC1',
                    y = 'PC2',
                    hue = df_pca['label'],
                    palette = ['red', 'green', 'blue'])

Observaciones finales

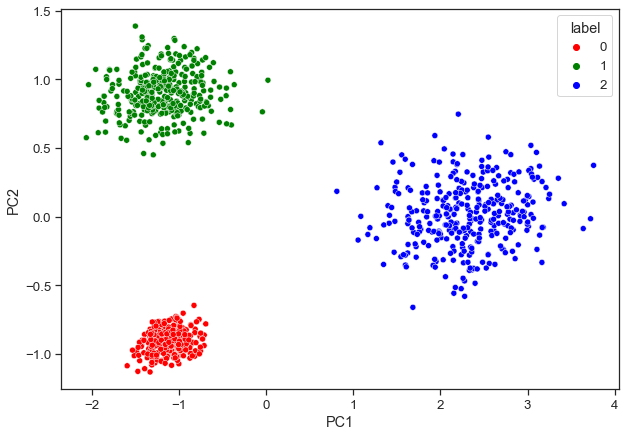
PCA es un concepto matemáticamente hermoso y espero poder transmitirlo en un tono informal para que no se sienta abrumador. Para aquellos que están ansiosos por ver los detalles esenciales, he adjuntado algunas discusiones/recursos interesantes a continuación para su lectura.