Evaluación de Modelos de Regresión Lineal
Publicado el: 15 de Febrero del 2021 - Jhonatan Montilla
En el siguiente caso de uso, se desea predecir el precio de una vivienda mediante el uso de funciones independientes o variables como promedio de renta de las personas, población de la zona y edad de la vivienda. Se determinará si las variables independientes fluctúan, para determinar si el precio de la vivienda también fluctúa. Por tanto, el objetivo principal es trazar la línea que mejor se ajuste a estas características (una línea recta). En la ciencia de datos, la mayoría de las cosas dependen de los datos, qué tipo de datos se utilizan, entonces para la regresión lineal se deben asumir algunas consideraciones sobre nuestros datos.
-
Se asume que la relación entre las variables dependientes e independientes es lineal, esto es un caso muy estraño en los datos del mundo real.
-
Los datos deben ser independientes.
-
En el modelo se asume que no hay multicolinealidad en los datos.
La matemática detrás de un algoritmo de Regresión Lineal.
y = mx + c (aquí la ecuación de la recta)
Y: Es lo que queremos predecir o variable dependiente, X: Value (variable independiente) nos ayudará a predecir el valor de Y, m: Es la pendiente de la línea y, C: Es la intersección del eje Y.
-
Regresión lineal simple: Predice la salida usando una sola característica.
-
Regresión lineal múltiple: Predice la salida utilizando múltiples funciones.
Usos de la regresión lineal.
Análisis predictivo.
El análisis predictivo pronostica oportunidades y riesgos futuros es la aplicación más destacada del análisis de regresión en los negocios. El análisis de la demanda, por ejemplo, predice la cantidad de artículos que probablemente comprará un consumidor.
Eficiencia operativa.
Los Modelos de Regresión Lineal también se pueden utilizar para optimizar los procesos de negocio. En un call center se puede analizar la relación entre los tiempos de espera de las personas que llaman y el número de quejas. La toma de decisiones basada en datos elimina las conjeturas, las hipótesis y las políticas corporativas en la toma de decisiones.
Decisiones de apoyo.
La regresión lineal no solo es excelente para brindar apoyo empírico a las decisiones de gestión, sino también para identificar errores de juicio. Un empleado en una gerencia puede pensar que al extender las compras aumentará las ventas, sin embargo, un modelo de regresión lineal podría indicar que el aumento de los ingresos puede no ser suficiente para respaldar el aumento de los cargos laborales adicionales de los empleados para la Empresa.
Nuevas perspectivas.
Como los datos son inútiles sin un análisis adecuado, es necesario aplicar técnicas de análisis de regresión con el objetivo de encontrar la relación entre diferentes variables al descubrir patrones que antes pasaban desapercibidos.
Caso de estudio.
Se comienza con la carga de los módulos de python necesarios y el conjunto de datos el cual podrá descargar directamente desde nuestro repositorio haciendo clic aquí.
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
df = pd.read_csv("ecommerce_customers.csv")
Descripción de Variables
- Email: Correo electrónico del cliente
- Address: Dirección de habitación del cliente
- Avg. Session Lenght: Tiempo promedio en que el cliente permanece conectado (en minutos)
- Time on App: Tiempo total en que el cliente se conecta através de la aplicación (en minutos)
- Time on Website: tiempo total en que el cliente se conecta a través del portal web (en minutos)
- Length of Membership: Tiempo de la menbresía del cliente (en meses)
- Yearly Amount Spent: Cantidad de dinero que ha gastado en cliente anualmente con el servicio de la Empresa (en USD).
round(df.head(),2)
| Address | Avatar | Avg. Session Length | Time on App | Time on Website | Length of Membership | Yearly Amount Spent | ||
|---|---|---|---|---|---|---|---|---|
| 0 | mstephenson@fernandez.com | 835 Frank Tunnel\nWrightmouth, MI 82180-9605 | Violet | 34.50 | 12.66 | 39.58 | 4.08 | 587.95 |
| 1 | hduke@hotmail.com | 4547 Archer Common\nDiazchester, CA 06566-8576 | DarkGreen | 31.93 | 11.11 | 37.27 | 2.66 | 392.20 |
| 2 | pallen@yahoo.com | 24645 Valerie Unions Suite 582\nCobbborough, D... | Bisque | 33.00 | 11.33 | 37.11 | 4.10 | 487.55 |
| 3 | riverarebecca@gmail.com | 1414 David Throughway\nPort Jason, OH 22070-1220 | SaddleBrown | 34.31 | 13.72 | 36.72 | 3.12 | 581.85 |
| 4 | mstephens@davidson-herman.com | 14023 Rodriguez Passage\nPort Jacobville, PR 3... | MediumAquaMarine | 33.33 | 12.80 | 37.54 | 4.45 | 599.41 |
Cantidad de Clientes registrados.
df['Avatar'].unique
<bound method Series.unique of 0 Violet
1 DarkGreen
2 Bisque
3 SaddleBrown
4 MediumAquaMarine
...
495 Tan
496 PaleVioletRed
497 Cornsilk
498 Teal
499 DarkMagenta
Name: Avatar, Length: 500, dtype: object>
Revisión de tipos de variables en el conjunto de datos.
- 4 variables de tipo objeto
- 5 variables de tipo numérico decimal
df.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 500 entries, 0 to 499 Data columns (total 8 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 Email 500 non-null object 1 Address 500 non-null object 2 Avatar 500 non-null object 3 Avg. Session Length 500 non-null float64 4 Time on App 500 non-null float64 5 Time on Website 500 non-null float64 6 Length of Membership 500 non-null float64 7 Yearly Amount Spent 500 non-null float64 dtypes: float64(5), object(3) memory usage: 25.5+ KB
Revisión de datos estadísticos
En esta sección se revisan algunos datos estadísticos contenidos en el conjunto de datos.
Respecto a la cantidad de dinero invertida por el cliente
- La máxima cantidad de dinero gastado por un cliente en el servicio de la empresa es de: 765.52 USD
- En promedio los clientes gastan en el sevicio de la empresa: 499.31 USD
Respecto a la antiguedad de los clientes
- El cliente más antiguo de la Empresa tiene una membresía de: 6.92 meses
Respecto al tiempo de conexión de los clientes en la Aplicación
- El mayor lapso de tiempo que un cliente permanece conectado a través de la aplicación es de: 15.13 minutos
- El lapso de tiempo promedio que un cliente permanece conectado a través de la aplicación es de: 12.05 minutos
Respecto al tiempo de conexión de los clientes a través del portal web
- El mayor lapso de tiempo que un cliente permanece conectado a través del portal web es de: 40.01 minutos
- El lapso de tiempo promedio que un cliente permanece conectado a través del portal web es de: 37.06 minutos
round(df.describe(),2)
| Avg. Session Length | Time on App | Time on Website | Length of Membership | Yearly Amount Spent | |
|---|---|---|---|---|---|
| count | 500.00 | 500.00 | 500.00 | 500.00 | 500.00 |
| mean | 33.05 | 12.05 | 37.06 | 3.53 | 499.31 |
| std | 0.99 | 0.99 | 1.01 | 1.00 | 79.31 |
| min | 29.53 | 8.51 | 33.91 | 0.27 | 256.67 |
| 25% | 32.34 | 11.39 | 36.35 | 2.93 | 445.04 |
| 50% | 33.08 | 11.98 | 37.07 | 3.53 | 498.89 |
| 75% | 33.71 | 12.75 | 37.72 | 4.13 | 549.31 |
| max | 36.14 | 15.13 | 40.01 | 6.92 | 765.52 |
Análisis gráfico de distribución y correlación
- En la diagonal se pueden observar la distribución de los datos a través de los gráficos de histogramas
- En los diagramas de dispersión se pueden observar la correlación entre las distintas distribución de los datos para cada par de variables.
sns.pairplot(df);
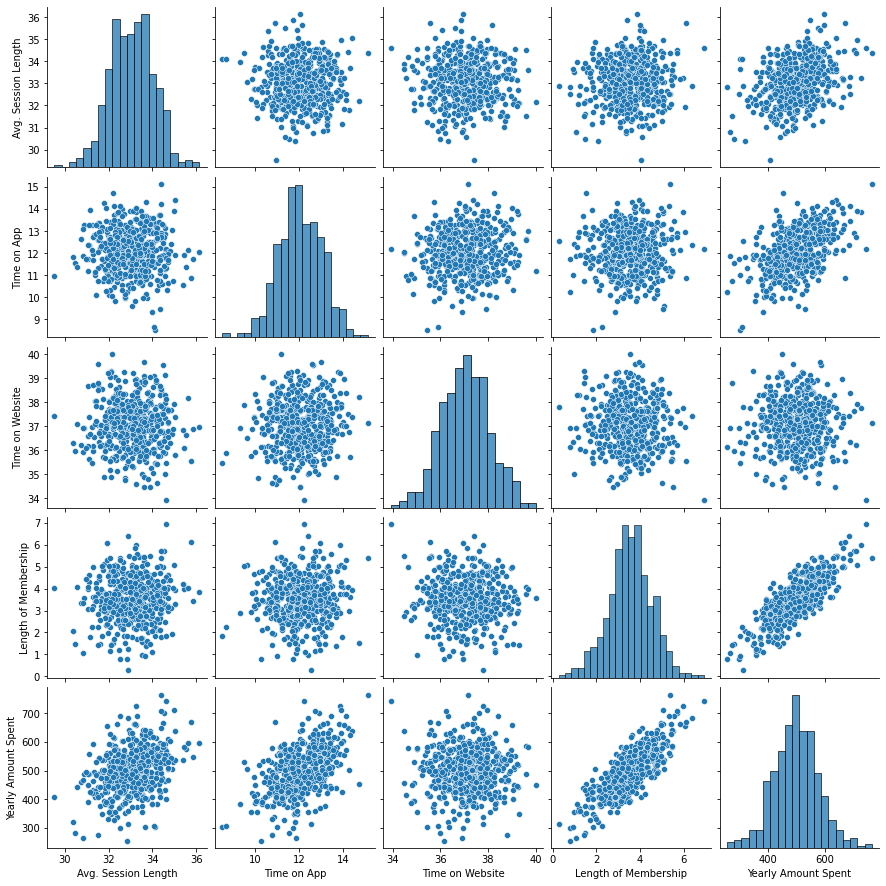
- Se puede observar claramente la correlación que existe entre las variables, tiempo de membresía de un cliente (Lenght of Membership) y la cantidad de dinero gastado por dicho cliente en los servicios de la Empresa en un año (Yearly Amount Spent).
Validación gráfica de la colinealidad
- Se puede observar visualmente la colinealidad entre las dos variables, a través de un segmento de recta que representa el modelo de regresión lineal.
sns.lmplot(x='Length of Membership',y='Yearly Amount Spent',data =df);
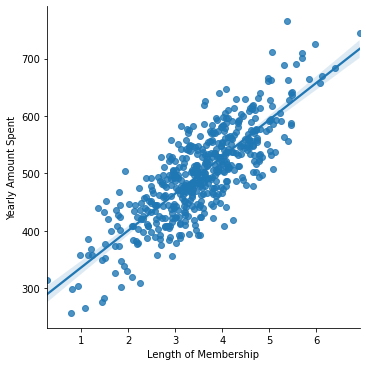
Preparación del conjunto de datos
- La variable objetivo a predecir es la cantidad de dinero que gasta un cliente en los servicio de la Empresa en un año (Yearly Amount Spent).
x = df[['Avg. Session Length','Time on App','Time on Website','Length of Membership']]
y = df['Yearly Amount Spent']
Separación de subconjuntos de datos, Entrenamiento y Pruebas
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.4)
Creación del Modelo de Regresión Lineal
lm = LinearRegression()
lm.fit(x_train,y_train)
LinearRegression()
Cálculo de los Coeficientes de Regresión
coeff_df = pd.DataFrame(lm.coef_,x.columns,columns=['Coefficient'])
round(coeff_df,2)
| Coefficient | |
|---|---|
| Avg. Session Length | 25.55 |
| Time on App | 38.49 |
| Time on Website | 0.48 |
| Length of Membership | 61.78 |
Predicciones del Modelo de Regresión Lineal
- A continuación se muestran a través de un gráfico de dispersión los datos predichos por el modelo
predictions = lm.predict(x_test)
plt.scatter(y_test,predictions);
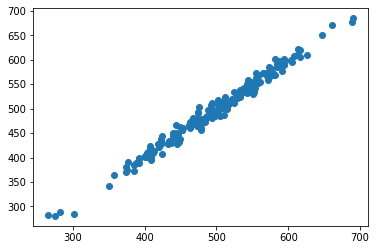
- A continuación los 5 primeros valores de la predicción del modelo.
predictions[:5]
array([557.10944853, 584.96471247, 573.30809474, 551.60732653,
427.58323562])
- A continuación los 5 primeros valores del conjunto de datos de pruebas
y_test.head()
294 557.634109 383 583.977802 435 571.216005 302 541.972204 444 423.470533 Name: Yearly Amount Spent, dtype: float64
¿Cómo se puede evaluar la efectividad de los modelos de regresión lineal?.
Error Absoluto Medio (Mean Absolute Error, MAE).
Es la diferencia absoluta promedio entre los resultados observados y pronosticados.
- error = actual − predicted
print('MAE:', round(mean_absolute_error(y_test, predictions),2))
MAE: 7.44
Conclusión.
- El modelo de regresión lineal tiene un error absoluto medio de 7.44USD, es decir, que en sus predicciones absolutas se equivoca en promedio casi siete dólares y medio en el monto que gastará un cliente en los servicios de la Empresa en un año.