 Volver al Inicio
Volver al Inicio
 Volver al Inicio
Volver al Inicio
20 de Septiembre del 2022 | Jhonatan Montilla
La probabilidad es el concepto central fundamental que se encuentra en la ciencia de datos, y la distribución de probabilidad es el tema principal en probabilidad. Por lo tanto, para dominar la ciencia de datos, ¡debe familiarizarse y sentirse cómodo con esas 10 distribuciones de probabilidad!
La distribución de Bernoulli es una distribución de probabilidad discreta que toma valor 1 con
probabilidad p y 0 con probabilidad 1-p. Intuitivamente, se puede pensar que tenemos una moneda
sesgada con una probabilidad p de salir adelante y 1-p de cruzar. La implementación de muestra
usando scipy.stats está a continuación:
from scipy.stats import bernoulli # Dist. Bernoulli
from scipy.stats import binom # Dist. Binomial
from scipy.stats import multinomial # Dist. Multinomial
from scipy.stats import norm # Dist. Normal
from scipy.stats import poisson # dist. Poisson
from scipy.stats import expon # Dist. Exponencial
from scipy.stats import beta # Dist. Beta
from scipy.stats import gamma # Dist. Gamma
from scipy.stats import chi2 # Dist Chi2
from scipy.stats import t # Dist. T de Student
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
# Parámetro de probabilidad especificado
p = 0.5
x = [i for i in range(0,10)]
# Muestra según la distribución de Bernoulli
y = bernoulli.rvs(p, size=10)
plt.plot(x,y, "ob")
plt.show()
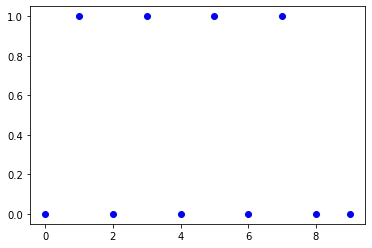
La distribución binomial es una generalización de la distribución de Bernoulli. En la distribución de Bernoulli, lanzamos la moneda una vez, pero puede pensar en la distribución binomial como experimentos de lanzamiento de n veces con probabilidad p de ser cara y 1-p de ser cruz cada vez. También es una variable aleatoria discreta que toma valores de 0 a n, donde n es el número de experimentos realizados. La probabilidad de obtener un número k se calcula mediante la siguiente fórmula:
En Python, podemos implementarlo de la siguiente manera:
# Parámetro de probabilidad especificado
p = 0.5
n = 10
x = [i for i in range(0,n)]
# Muestra según distribución Binomial
y = binom.rvs(n, p, size=10)
plt.plot(x,y, "ob")
plt.show()
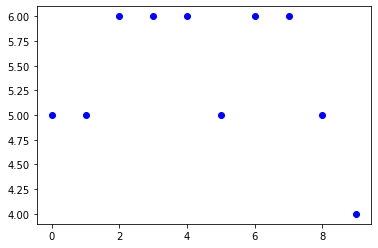
Como sugiere el nombre, la distribución multinomial está relacionada con la distribución binomial: de hecho, es una generalización de la distribución multinomial. En la distribución Binomial, solo tenemos 2 resultados posibles. ¿Qué pasa si nuestros experimentos tienen múltiples resultados? Una analogía es como si la distribución binomial estuviera lanzando una moneda 10 veces, mientras que la distribución multinomial es como elegir un número al azar de 1,2,3 con la probabilidad de p1, p2, p3=(1-p1-p2) . Su función de masa de probabilidad se ve así:
Donde n es el número de experimentos y x_i es el resultado del i-ésimo experimento.
Nuevamente, la implementación de python parece útil con la ayuda de scipy.stats:
# Parámetro de probabilidad especificado
p = [0.3,0.2,0.5]
n = 10
x = [i for i in range(0,n)]
# Muestra según distribución Multinomial
y = multinomial.rvs(n, p, size=10)
plt.plot(x,y, "ob")
plt.show()
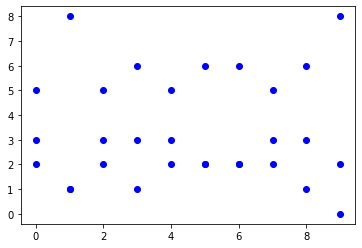
Si compara la imagen de la distribución multinomial y la de la distribución binomial, se verán similares excepto por cada valor de x, tendremos múltiples resultados aleatorios en el caso de la distribución multinomial. (¿Por qué hay 3 valores para x = 0 y 2 para x = 8? Bueno, la razón es que tenemos un valor duplicado para x = 8 y matplotlib no puede mostrarlo).
Si hay una distribución más importante que necesita aprender, esa debe ser la distribución de Gauss. Me puede llevar un semestre entero contarte la magia de esta clase. Desafortunadamente, este no es el lugar para hacerlo. Debe recordar que la distribución gaussiana incluye 2 parámetros: valor medio y desviación estándar. Esos dos valores determinarán las perspectivas de comportamiento de la distribución. El valor medio decidirá dónde se centrará la distribución, mientras que el parámetro de desviación estándar decidirá qué tan dispersa se verá su distribución. La probabilidad de obtener x de su experimento se verá así:
Aquí, σ será la desviación estándar y μ será el valor medio.
Nuevamente, se sigue la implementación de Python:
x1 = np.arange(-20, 20, 0.1)
y1 = norm.pdf(x1, 0, 5)
y2 = norm.pdf(x1, 0, 3)
y3 = norm.pdf(x1, 5, 3)
plt.plot(x1, y2)
plt.plot(x1, y1)
plt.plot(x1, y3)
plt.legend(["Desviación estándar 3",
"Desviación estándar 5",
"valor medio de 5"],
loc = 'upper left')
plt.show()
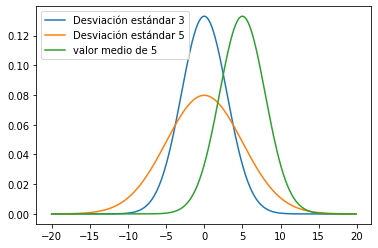
En lugar de dibujar los resultados de los experimentos, decidí mostrarle la forma de la función de masa de probabilidad de la distribución gaussiana, o simplemente la curva. Es precioso, y veréis como cambia la distribución con los cambios de parámetros.
La distribución de Poisson es una distribución discreta que describe la cantidad de eventos que ocurren en un tiempo fijo dada la frecuencia con la que ocurren esos eventos en promedio. Imagina que estás esperando un autobús. Se sabe que el autobús llega una vez cada 10 minutos en promedio, y desea saber cuál es la probabilidad de que vea la llegada de 2 autobuses en los próximos 20 minutos. Aquí es donde la distribución de Poisson puede ayudarlo.
La fórmula para calcular k eventos ocurrirán en la unidad de tiempo futura es la siguiente, donde λ es la ocurrencia promedio.
La implementación de Python de una distribución de Poisson está aquí:
# Parámetro de probabilidad especificado
mu = 2
n = 100
x = [i for i in range(0,n)]
# Muestra según distribución de Poisson
y = poisson.rvs(mu, size=n)
plt.plot(x,y, "ob")
plt.show()
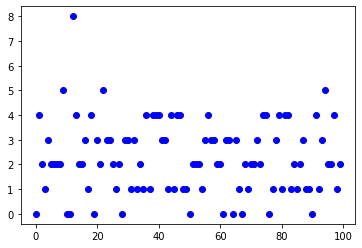
El código anterior simula cuántas ocurrencias obtendrá si su promedio es de 2 ocurrencias por unidad de tiempo. El resultado es el siguiente:
Puede ver que está fuertemente centrado en valores más bajos, pero ocasionalmente obtiene valores más altos. ¡También se puede aplicar a tu vida! Aunque en promedio, no sucederán demasiadas cosas buenas en un día, tendremos momentos en nuestras vidas en los que ocasionalmente sucederán muchas cosas buenas en un día. ¡Asi que preparate!
La distribución exponencial es en realidad la distribución dual de Poisson. En la distribución exponencial, nos interesa el valor del tiempo de espera hasta la siguiente ocurrencia, en lugar del número de ocurrencias. Para el ejemplo de la parada de autobús, ya no nos importa el número de llegadas en los próximos 20 minutos. Solo nos importa cuándo llegará el próximo autobús.
La probabilidad del tiempo de espera x se puede calcular mediante la fórmula: (nótese que x no puede ser negativo).
Su implementación en python se puede escribir de la siguiente manera:
# Parámetro de probabilidad especificado
mu = 2
n = 100
x = [i for i in range(0,n)]
# Muestra según distribución Exponencial
y = expon.rvs(scale=2, size=n)
plt.plot(x,y, "ob")
plt.show()
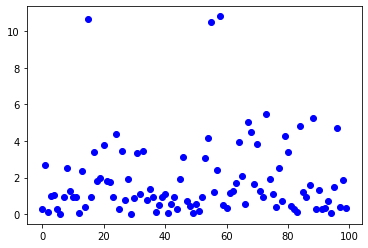
Aquí, en promedio, esperaremos 2 minutos en promedio, y veremos nuestro tiempo de espera en el futuro 100 espera el autobús.
Aún así, tendremos algo de mala suerte, pero la mayoría de los casos deberían durar menos de 4 minutos.
La distribución beta es una distribución variable aleatoria continua sobre [0,1] interno. Tiene dos parámetros α y β. α y β, al igual que la media y la desviación estándar en la distribución gaussiana, controlan la forma de la distribución. Están relacionados con el tamaño y la media de la muestra, pero la relación en sí es más complicada que la “igualdad”. La distribución beta se usa a menudo en la inferencia bayesiana como distribución previa. Los detalles de eso no se pueden explicar en unas pocas oraciones, pero una descripción general de alto nivel de lo anterior es lo que espera antes de ejecutar los experimentos aleatorios. Por ejemplo, si vas a ver a un jugador de fútbol, no debes esperar que pueda marcar más de 5 goles en este partido. Probablemente 0.5–1.5 puede ser un buen rango de conjetura para eso. El anterior puede considerarse como un "rango de adivinanzas" matemáticamente más riguroso. La función de densidad de probabilidad no es particularmente importante, por lo que solo se mostrará la implementación:
# Parámetro de probabilidad especificado
a = 2
b = 3
n = 100
x = [i for i in range(0,n)]
# Muestra según distribución Beta
y = beta.rvs(a, b, size=n)
plt.plot(x,y, "ob")
plt.show()
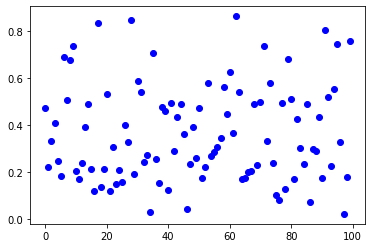
Un sorteo aleatorio de muestra según la distribución beta se verá así:
Like Beta distribution, Gamma distribution is also two-parameter continuous probability distribution, and it is also a good model for prior distribution. It is a conjugate prior function for many distributions: Gaussian distribution, Poisson distribution, etc. Some special case of gamma distribution includes the Exponential distribution mentioned above and the Chi-square distribution to be discussed after. Besides that, it also has an interesting link to information theory: among all some distributions, the Gamma distribution has the maximum entropy. If you are interested in the details, feel free to explore more!
Again, Python implementation:
# Parámetro de probabilidad especificado
a = 2
b = 3
n = 100
x = [i for i in range(0,n)]
# Muestra según distribución Gamma
y = gamma.rvs(a, b, size=n)
plt.plot(x,y, "ob")
plt.show()
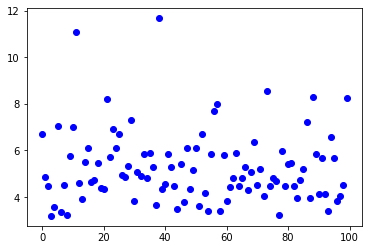
Puede ver que la distribución Gamma tiene un patrón bastante diferente al de la distribución Beta.
La distribución Chi-cuadrado pertenece a una de las distribuciones más importantes y conocidas para científicos de datos y estadísticos. Aparece en numerosos entornos estadísticos: prueba de independencia de chi-cuadrado, calidad de ajuste de chi-cuadrado entre los datos y la distribución propuesta, prueba de razón de verosimilitud, etc. Su importancia no se puede subestimar. Es una distribución de probabilidad continua en (0, infinito), y también es un caso especial de distribución Gamma. El parámetro que toma se llama grados de libertad y, como es habitual, este parámetro determinará la forma de la distribución.
En Python, podemos ver la forma de distribución:
# Parámetro de probabilidad especificado
df1 = 10
df2 = 20
df3 = 30
df4 = 40
df5 = 50
# calcular el rango que queremos mostrar
x = np.linspace(0,
30,
500)
# Muestra según distribución chi2
rv1 = chi2(df1)
rv2 = chi2(df2)
rv3 = chi2(df3)
rv4 = chi2(df4)
rv5 = chi2(df5)
plt.plot(x, rv1.pdf(x), 'r', label='df = 10')
plt.plot(x, rv2.pdf(x), 'g',label='df = 20')
plt.plot(x, rv3.pdf(x), 'b', label='df = 30')
plt.plot(x, rv4.pdf(x), 'black',label='df = 40')
plt.plot(x, rv5.pdf(x), 'yellow',label='df = 50')
plt.legend(loc="upper left")
plt.show()
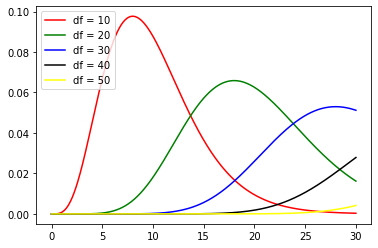
Otra cosa que los científicos de datos usan a menudo es la prueba de Chi-cuadrado, que se usa especialmente para calcular la aptitud de los datos de muestreo dada la distribución propuesta o la prueba de independencia. En scipy.stats, podemos calcular fácilmente la estadística de prueba Chi-squared mediante scipy.stats.chisquare(your_sample, added_distribution) . ¡Es súper fácil de usar!
Finalmente, llegamos a la distribución t de Student. Es otra distribución muy utilizada en pruebas estadísticas. Se originó a partir del problema de estimar el parámetro medio de la distribución gaussiana con un parámetro de desviación estándar desconocido dado un conjunto de datos de muestra. Posteriormente, se aplica ampliamente a muchos entornos estadísticos, como la construcción de intervalos de confianza y el análisis de regresión. Su forma se parece mucho a la distribución gaussiana con la excepción de que tiene colas más pesadas (más dispersas que la distribución normal). Al igual que la distribución de Chi-cuadrado, también incluye un parámetro, generalmente también denominado grado de libertad. Como era de esperar, el DoF también controla la forma de la distribución.
Una visualización de Python es la siguiente:
# Parámetro de probabilidad especificado
df1 = 1
df2 = 2
df3 = 3
df4 = 4
# calcular el rango que queremos mostrar
x = np.linspace(-10,
10,
200)
# Muestra según distribución t
rv1 = t(df1)
rv2 = t(df2)
rv3 = t(df3)
rv4 = t(df4)
plt.plot(x, rv1.pdf(x), 'r', label='df = 10')
plt.plot(x, rv2.pdf(x), 'g',label='df = 20')
plt.plot(x, rv3.pdf(x), 'b', label='df = 30')
plt.plot(x, rv4.pdf(x), 'black',label='df = 40')
plt.plot(x, norm.pdf(x), 'yellow', label='Gaussian')
plt.legend(loc="upper left")
plt.show()
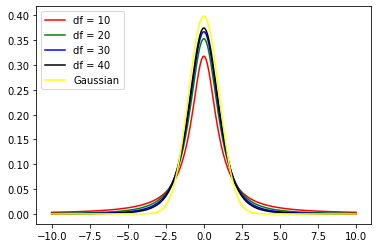
Deliberadamente puse la distribución gaussiana en la imagen para que pueda tener una visión clara de su diferencia. Se puede ver que la distribución gaussiana tiene colas más pequeñas que la distribución t, así como picos más grandes.
Al igual que en la distribución Chi-cuadrado, también podemos hacer una prueba t usando Python. En el siguiente fragmento de código, hacemos una prueba t para comprobar si la muestra proviene de dos distribuciones diferentes o no.
seed = np.random.default_rng()
# Verdad básica: muestreo de la misma distribución
rvs1 = stats.norm.rvs(loc = 5,
scale =10,
size = 500,
random_state = seed
)
rvs2 = stats.norm.rvs(loc = 5,
scale = 10,
size = 500,
random_state = seed
)
print(stats.ttest_ind(rvs1, rvs2))
# Ejemplo de respuesta, varía mucho No se puede decir
# nada definitivo del resultado dado el valor p
# Ttest_indResult(statistic=-0.7362272777889193,
# pvalue=0.46176540317360304)
rvs3 = stats.norm.rvs(loc = 0,
scale = 10,
size = 500,
random_state = seed
)
print(stats.ttest_ind(rvs1, rvs3))
# Respuesta de muestra, varía mucho Podemos decir con
# mucha confianza que dos datos no son de la misma
# distribución
# Ttest_indResult(statistic = 8.065543453125999,
# pvalue = 2.078369795336982e-15)
Ttest_indResult(statistic=0.15019938905647343, pvalue=0.8806376574425193) Ttest_indResult(statistic=7.761945071408706, pvalue=2.0640142442347023e-14)
Puede ver en los comentarios que el t-square es bastante preciso en el resultado. (Aquí, el valor p puede determinar la confianza de la prueba, y vemos que la prueba t nos dice que rvs1 y rvs2 no son del mismo lugar, lo que coincide con la verdad).