Asimetría y Curtosis en la distribución de Datos
Publicado el: 09 de Diciembre del 2020 - Jhonatan Montilla
En este artículo, se repasarán dos conceptos importantes de la estadística descriptiva: La Asimetría y la Curtosis, al concluir este artículo se obtendrán respuestas a preguntas como, ¿qué es asimetría derecha e izquierda?, ¿Cómo se miden, la Asimetría y Curtosis?, su utilidad y su aplicación.
La Asimetría
La "asimetría" es una medida de la distribución de probabilidad de una variable aleatoria de valor real.
Sesgo negativo
Se considera una distribución de datos con sesgo negativo cuando la mayoría de los datos que se concentran más a la derecha en una repreesentación gráfica de histograma, la cual se mostrará más adelante en este artículo. Entonces, en esta distribución existe una "cola" larga en el lado izquierdo de la gráfica, también se denomina, sesgado a la izquierda, o "cola a la izquierda".
Sesgo positivo
Se considera una distribución de datos con sesgo positivo cuando la mayoría de los datos se concentran más a la izquierda del histograma, Esta distribución muestra una "cola" larga en el lado derecho, también se denomina sesgado a la derecha o de "cola a la derecha".
Cómo interpretar la asimetría
Una regla general establece:
- Si la asimetría está entre -0,5 y 0,5, los datos son bastante simétricos (distribución normal).
- Si la asimetría está entre -1 y -0,5 (sesgo negativo) o entre 0,5 y 1 (sesgo positivo), los datos están moderadamente sesgados.
- Si el sesgo es menor que -1 (sesgo negativo) o mayor que 1 (sesgo positivo), los datos están muy sesgados.
Si los datos siguen una distribución normal, su asimetría será cero. Pero en el mundo real, no encontramos ningún dato que siga perfectamente la distribución normal. Por lo tanto, para los datos del mundo real, no encontramos una asimetría exacta de cero, pero puede ser cercana a cero.
En el siguiente ejemplo, se utilizará el conjunto de datos de la librería Seaborn, como primer paso se cargarán las librerías necesarias.
import numpy as np
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use('ggplot')
from scipy.stats import skew
from seaborn import load_dataset
from scipy.stats import skew, kurtosis
from sklearn.datasets import load_boston
Se procede con la carga del conjunto de datos y se muestran las primeras filas contenidas en el mismo.
df = load_dataset('tips')
df.head()
| total_bill | tip | sex | smoker | day | time | size | |
|---|---|---|---|---|---|---|---|
| 0 | 16.99 | 1.01 | Female | No | Sun | Dinner | 2 |
| 1 | 10.34 | 1.66 | Male | No | Sun | Dinner | 3 |
| 2 | 21.01 | 3.50 | Male | No | Sun | Dinner | 3 |
| 3 | 23.68 | 3.31 | Male | No | Sun | Dinner | 2 |
| 4 | 24.59 | 3.61 | Female | No | Sun | Dinner | 4 |
sns.histplot(df['total_bill']);
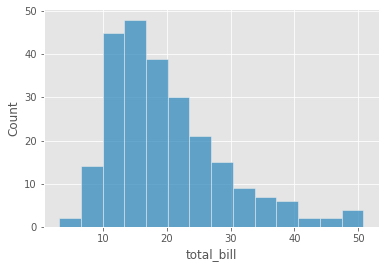
Por qué estudiar la asimetría¶
En el gráfico de ejemplo anterior, los datos de la variable total_bill están positivamente sesgados, la mayoría de los registros de datos se concentran en el lado izquierdo. Por lo tanto, si se tuviese que construir un modelo sobre estos datos, dicho modelo hará mejores predicciones donde total_bill es menor en comparación con los valores de total_bill más altos.
La asimetría es un factor que indica en cierta medida la dirección de los valores atípicos. Por lo tanto, de la distribución mostrada anteriormente se podría concluir claramente que los valores atípicos se encuentran presentes en el lado derecho de la distribución.
skew(df['total_bill'])
1.1262346334818638
Como se pudo observar, total_bill tiene un sesgo de 1,12, lo que significa que la distribución de los datos se encuentran sesgados positivamente, también es notoriamente visible observar la gráfica de distribución anterior.
Cómo lidiar con datos sesgados¶
Muchas pruebas estadísticas y modelos de aprendizaje automático dependen de supuestos de normalidad. Entonces, una asimetría significativa significa que los datos no son normales y eso puede afectar sus pruebas estadísticas o el poder de predicción del aprendizaje automático. En tales casos, necesitamos transformar los datos para que sean normales. Algunas de las técnicas comunes utilizadas para tratar datos asimétricos:
- Transformación Logaritmica
- Transformación Raíz Cuadrada
- Transformación Exponencial
- Transformación Box-Cox, etc.
Transformación Logarítmica¶
Para reducir el sesgo positivo de dicha distribución se procede a realizar una transformación logarítmica de los datos para hacer normal su distribución, tal como se muestra a continuación.
sns.histplot(np.log(df['total_bill'])); # transformación logarítmica de registros
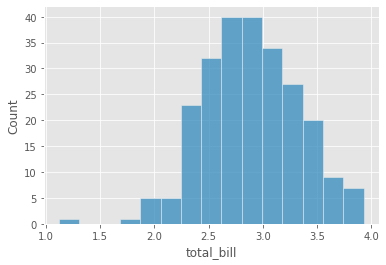
skew(np.log(df['total_bill']))
-0.1155150356541124
Después de la transformación logarítmica de la variable total_bill, la asimetría se reduce a -0,12, esto significa que actualmente es muchísimo más simétrica que el caso anterior, lo que permitirá obtener mejores resultados de predicción al momento de entrenar a un modelo de aprendizaje automático.
La Curtosis.¶
La "curtosis" es la longitud medida de la "cola" de la distribución de probabilidad de una variable aleatoria de valor real. Generalmente se utiliza para identificar valores atípicos (valores anómalos) en un conjunto de datos, debido a que se utiliza para identificar valores atípicos, los valores extremos en ambas lados de las colas se utilizan para el análisis.
Tipos de Curtosis y cómo interpretarlos¶
Para los siguientes ejemplos se utilizará el conjunto de datos "boston" de la librería Seaborn con el cual se mostrará cómo calcular los distintos tipos de curtosis:
boston = load_boston()
X = pd.DataFrame(boston['data'], columns=boston['feature_names'])
y = boston['target']
X.head()
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 |
A continuación se muestra la distribución de la variable CRIM del conjunto de datos.
sns.histplot(X['CRIM']);
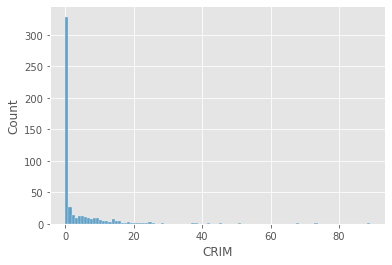
kurtosis(X['CRIM'])
36.75278626142281
Leptocúrtica (Curtosis > 3)¶
-
Esta distribución muestra mayor curtosis que mesocúrtica. El pico es más alto y agudo que el mesokurtico. Muestra colas pesadas hacia un lado o en algunos casos a ambos lados que indican valores atípicos grandes.
-
En el mundo de las inversiones una distribución leptocúrtica significa que es una inversión de alto riesgo.
A continuación se muestra la distribución de la variable AGE del conjunto de datos.
sns.histplot(X['AGE']);
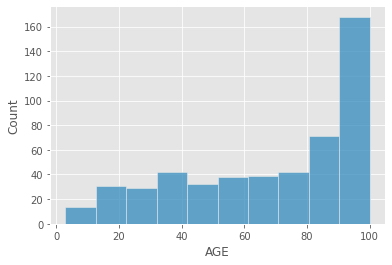
kurtosis(X['AGE'])
-0.97001392664039
Platicúrtica: (Curtosis < 3)¶
-
Esta distribución muestra una menor curtosis que la mesocúrtica. El pico es más bajo y más ancho que Mesokurtic. Muestra colas planas a ambos lados que indican pequeños valores atípicos.
-
En el mundo de las inversiones una distribución platicúrtica significa que es una inversión de bajo riesgo.
sns.histplot(X['RM']);
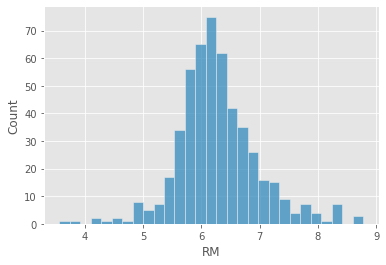
kurtosis(X['RM'])
1.8610269725310244
Mesocúrtica (Curtosis = 3):¶
- Esta distribución muestra una curtosis de 3 cerca de cero. La distribución de valores extremos (valores atípicos) es similar a la de la distribución normal.