 Volver al Inicio
Volver al Inicio
 Volver al Inicio
Volver al Inicio
10 de Enero del 2023 | Jhonatan Montilla
En la ciencia de datos, una tarea común es la detección de anomalías, es decir, comprender si una observación es "inusual". En primer lugar, ¿qué significa ser inusual? En este artículo vamos a inspeccionar tres formas diferentes en las que una observación puede ser inusual: puede tener características inusuales, puede que no se ajuste bien al modelo o puede ser particularmente influyente en el entrenamiento del modelo. Veremos que en la regresión lineal la última característica es un subproducto de las dos primeras.
Es importante destacar que ser inusual no es necesariamente malo. Las observaciones que tienen características diferentes de todas las demás a menudo contienen más información. También esperamos que algunas observaciones no se ajusten bien al modelo, de lo contrario, el modelo probablemente esté sesgado (estamos sobreajustando). Sin embargo, es más probable que las observaciones “inusuales” sean generadas por un proceso de generación de datos diferente. Los casos extremos incluyen error de medición o fraude, pero otros casos pueden tener más matices, como usuarios genuinos con características o comportamientos raros. El conocimiento del dominio siempre es el rey y descartar observaciones solo por razones estadísticas nunca es prudente.
Dicho esto, echemos un vistazo a algunas formas diferentes en las que las observaciones pueden ser "inusuales".
Supongamos que fuéramos una plataforma en línea peer-to-peer y estuviéramos interesados en saber si hay algo sospechoso en nuestro negocio. Tenemos información sobre cuánto tiempo pasan nuestros usuarios en la plataforma y el valor total de sus transacciones.
%run dgp.py
%run utils.py
# from src.utils import *
# from src.dgp import dgp_p2p
df = dgp_p2p().generate_data()
df.head()
| Horas | Transacciones | |
|---|---|---|
| 0 | 2.6 | 8.30 |
| 1 | 2.0 | 8.00 |
| 2 | 7.0 | 21.00 |
| 3 | 6.7 | 18.00 |
| 4 | 1.2 | 3.82 |
Contamos con información de 50 usuarios para los cuales observamos horas de permanencia en la plataforma y monto total de transacciones. Como solo tenemos dos variables, podemos inspeccionarlas fácilmente usando un diagrama de dispersión.
sns.scatterplot(data=df,
x='Horas',
y='Transacciones').set(title='Diagrama de dispersión de datos');
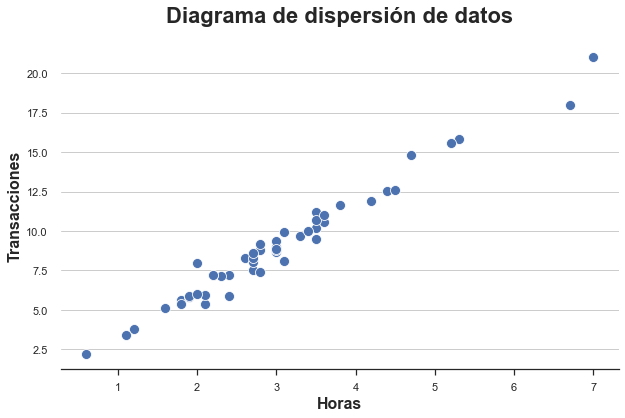
La relación entre horas y transacciones parece seguir una clara relación lineal. Si ajustamos un modelo lineal, observamos un ajuste particularmente ajustado.
smf.ols('Horas ~ Transacciones', data=df).fit().summary().tables[1]
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -0.0975 | 0.084 | -1.157 | 0.253 | -0.267 | 0.072 |
| Transacciones | 0.3452 | 0.009 | 39.660 | 0.000 | 0.328 | 0.363 |
La primera métrica que vamos a utilizar para evaluar las observaciones "inusuales" es el apalancamiento. El objetivo del apalancamiento es capturar cuánto es diferente un solo punto con respecto a otros puntos de datos. Estos puntos de datos a menudo se denominan valores atípicos y existe una cantidad casi infinita de algoritmos y reglas generales para marcarlos. Sin embargo, la idea es la misma: marcar las observaciones que son inusuales en términos de características.
Algebraicamente, el apalancamiento de la observación i es el elemento iₜₕ de la matriz de diseño X’(X’X)⁻¹X. Entre las muchas propiedades de los apalancamientos, está el hecho de que no son negativos y sus valores suman la dimensión de X (en nuestro caso 1).
Calculemos el apalancamiento de las observaciones en nuestro conjunto de datos. También marcamos las observaciones que tienen apalancamientos inusuales (que definimos arbitrariamente como más de dos desviaciones estándar del apalancamiento promedio).
Tracemos la distribución de los valores de apalancamiento en nuestros datos.
X = np.reshape(df['Horas'].values, (-1, 1))
Y = np.reshape(df['Transacciones'].values, (-1, 1))
df['Apalancamiento'] = np.diagonal(X @ np.linalg.inv(X.T @ X) @ X.T)
df['Alto_Apalancamiento'] =
df['Apalancamiento'] > (np.mean(df['Apalancamiento']) + 2*np.std(df['Apalancamiento']))
fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))
sns.histplot(data=df,
x='Apalancamiento',
hue='Alto_Apalancamiento',
alpha=1,
bins=30,
ax=ax1).set(title='Distribución de Apalancamientos');
sns.scatterplot(data=df,
x='Horas',
y='Transacciones',
hue='Alto_Apalancamiento',
ax=ax2).set(title='Diagrama de Dispersión de Datos');
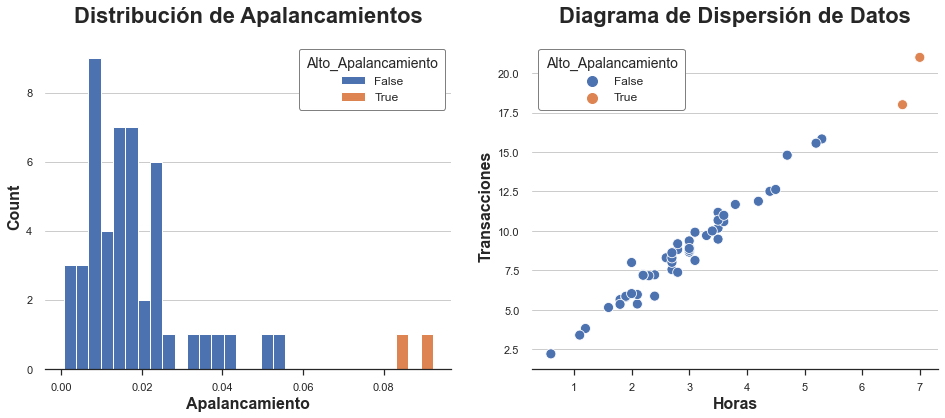
Como podemos ver, la distribución está sesgada, con dos observaciones que tienen un apalancamiento inusualmente alto. De hecho, en el diagrama de dispersión, estas dos observaciones están ligeramente separadas del resto de la distribución.
¿Son malas noticias? Eso depende. Los valores atípicos no son un problema per se. En realidad, si son observaciones genuinas, pueden contener mucha más información que otras observaciones. Por otro lado, también es más probable que no sean observaciones genuinas (p. ej., fraude, error de medición, etc.) o que sean inherentemente diferentes de las demás (p. ej., usuarios profesionales frente a aficionados). En cualquier caso, es posible que deseemos investigar más a fondo y utilizar tanta información específica del contexto como podamos.
Es importante destacar que el hecho de que una observación tenga un alto apalancamiento nos brinda información sobre las características del modelo, pero nada sobre el modelo en sí. ¿Son estos usuarios simplemente diferentes o también se comportan de manera diferente?
Hasta ahora solo hemos hablado de características inusuales, pero ¿qué pasa con el comportamiento inusual? Esto es lo que miden los residuos de la regresión.
Los residuos de regresión son la diferencia entre los valores de resultado previstos y los valores de resultado observados. En cierto sentido, capturan lo que el modelo no puede explicar: cuanto mayor sea el residuo de una observación, más inusual es en el sentido de que el modelo no puede explicarlo.
Y_hat = X @ np.linalg.inv(X.T @ X) @ X.T @ Y
plt.scatter(X, Y, s=50, label='Datos')
plt.plot(X, Y_hat, c='k', lw=2, label='Predicción')
plt.vlines(X,
np.minimum(Y, Y_hat),
np.maximum(Y,Y_hat),
color='r', lw=3, label="Residuos");
plt.legend()
plt.title(f"Predicción de Regresión y Residuos");
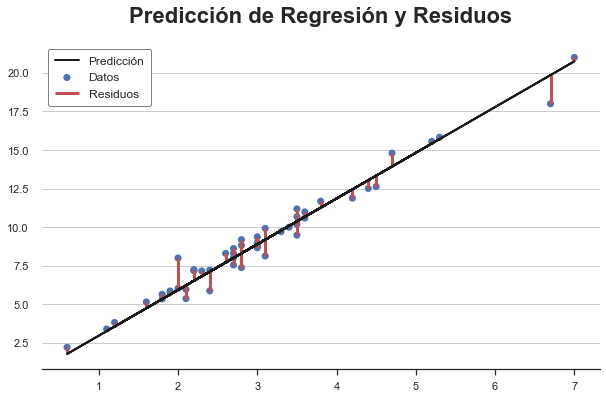
Dos observaciones tienen residuos particularmente altos. Esto significa que para estas observaciones, el modelo no es bueno para predecir los resultados observados.
¿Son malas noticias? De nuevo, no necesariamente. Es probable que un modelo que se ajuste demasiado bien a las observaciones esté sesgado. Sin embargo, aún puede ser importante comprender por qué algunos usuarios tienen una relación diferente entre las horas dedicadas y las transacciones totales. Como de costumbre, el conocimiento del dominio es clave.
Hasta ahora, hemos analizado observaciones con características "inusuales" y comportamiento "inusual", en términos de un modelo. Pero, ¿de dónde viene el modelo? ¿Cuánto de nuestro modelo está impulsado por un puñado de observaciones? ¿Cuáles?
El concepto de influencia y funciones de influencia se desarrolló precisamente para responder a esta pregunta: ¿qué son las observaciones influyentes? Esta pregunta fue muy popular en los años 80 y perdió atractivo durante mucho tiempo hasta hace poco, debido a la creciente necesidad de explicar modelos complejos de aprendizaje automático e IA.
Como puede ver, existe una estrecha conexión tanto con el apalancamiento hᵢᵢ como con los residuos eᵢ: la influencia está aumentando en ambos. De hecho, en la regresión lineal, las observaciones con alto apalancamiento son observaciones que son atípicas y tienen residuos altos. Ninguna de las dos condiciones por sí sola es suficiente para que una observación influya en el modelo.
Podemos verlo mejor en los datos.
df['Residuos'] = np.abs(Y - X @ np.linalg.inv(X.T @ X) @ X.T @ Y)
df['Alto_Residuos'] = df['Residuos'] > (np.mean(df['Residuos']) + 2*np.std(df['Residuos']))
df['Influencia'] = (np.linalg.inv(X.T @ X) @ X.T).T * np.abs(Y - Y_hat)
df['Alta_Influencia'] =
df['Influencia'] > (np.mean(df['Influencia']) + 2*np.std(df['Influencia']))
fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(16,6))
sns.histplot(data=df,
x='Influencia',
hue='Alta_Influencia',
alpha=1,
bins=30,
ax=ax1).set(title='Distribución de Influencias');
sns.scatterplot(data=df,
x='Horas',
y='Transacciones',
hue='Alta_Influencia',
ax=ax2).set(title='Diagrama de Dispersión de Datos');
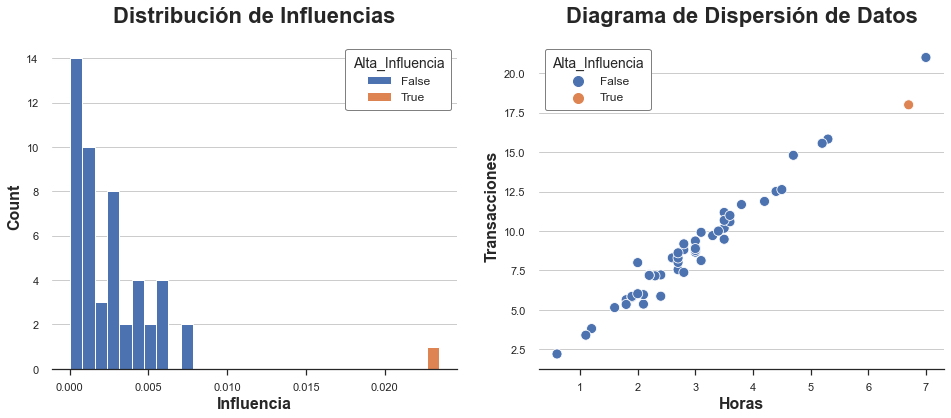
En nuestro conjunto de datos, solo hay una observación con gran influencia y su valor es desproporcionadamente mayor que la influencia de todas las demás observaciones. ¿Lo hubieras adivinado solo a partir del diagrama de dispersión?
Ahora podemos trazar todos los puntos "inusuales" en el mismo gráfico. También informo los residuos y el apalancamiento de cada punto en un gráfico separado.
def plot_leverage_residuals(df):
# Hue
df['Tipo'] = 'Normal'
df.loc[df['Alto_Residuos'], 'Tipo'] = 'Alto_Residuos'
df.loc[df['Alto_Apalancamiento'], 'Tipo'] = 'Alto_Apalancamiento'
df.loc[df['Alta_Influencia'], 'Tipo'] = 'Alta_Influencia'
# Init figure
fig, (ax1,ax2) = plt.subplots(1,2, figsize=(12,5))
ax1.plot(X, Y_hat, lw=1, c='grey', zorder=0.5)
sns.scatterplot(data=df, x='Horas',
y='Transacciones', ax=ax1, hue='Tipo').set(title='Datos')
sns.scatterplot(data=df, x='Residuos', y='Apalancamiento',
hue='Tipo', ax=ax2).set(title='Métricas')
ax1.get_legend().remove()
plt.legend(bbox_to_anchor=(1.05, 0.8), loc='upper left', borderaxespad=0);
plot_leverage_residuals(df)
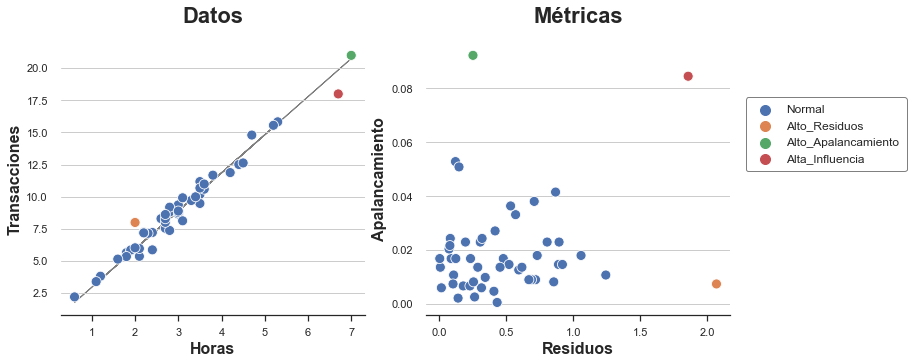
Como podemos ver, tenemos un punto con alto apalancamiento y bajo apalancamiento, otro con alto apalancamiento y bajo residual, y solo un punto con alto apalancamiento y alto residual: el único punto influyente.
De la gráfica también queda claro por qué ninguna de las dos condiciones por sí sola es suficiente para que una observación influya y distorsione el modelo. El punto naranja tiene un residual alto pero se encuentra justo en el medio de la distribución y por lo tanto no puede inclinar la línea de mejor ajuste. En cambio, el punto verde tiene un gran apalancamiento y se encuentra lejos del centro de la distribución, pero está perfectamente alineado con la línea de ajuste. Eliminarlo no cambiaría nada. En cambio, el punto rojo es diferente de los demás en términos de características y comportamiento y, por lo tanto, inclina la línea de ajuste hacia sí mismo.
En esta publicación, hemos visto un par de formas diferentes en las que las observaciones pueden ser "inusuales": pueden tener características inusuales o un comportamiento inusual. En la regresión lineal, cuando una observación tiene ambas también influye: inclina el modelo hacia sí mismo.
En el ejemplo del artículo, nos concentramos en una regresión lineal univariada. Sin embargo, la investigación sobre las funciones de influencia se ha convertido recientemente en un tema candente debido a la necesidad de hacer que los algoritmos de aprendizaje automático de caja negra sean comprensibles. Con modelos con millones de parámetros, miles de millones de observaciones y no linealidades salvajes, puede ser muy difícil establecer si una sola observación es influyente y cómo.